Seja P a imagem de um ângulo θ no ciclo trigonométrico. Define-se o seno do ângulo θθ como a ordenada de P e o cosseno de θ como a abscissa de P.
Assim, para obter o seno de θ, devemos projetar P sobre o eixo vertical Oy, denominado eixo dos senos, e, para obter o cosseno de θ, devemos projetar P sobre o eixo horizontal Ox, denominado eixo dos cossenos. Na figura a seguir, temos:
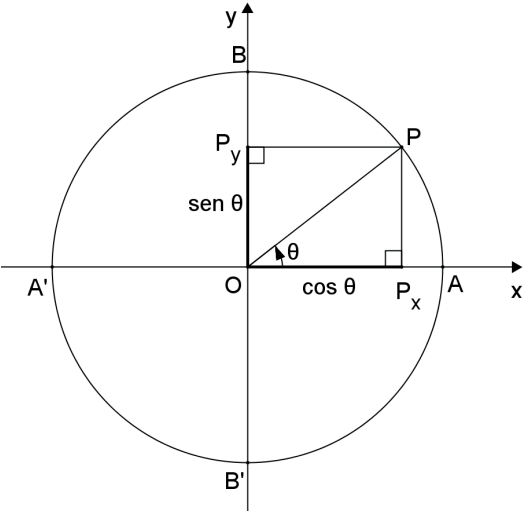
sen θ = O̲P̲y
cos θ = O̲P̲x
Observe que, O̲P̲y e O̲P̲x são segmentos orientados.
Dessa forma, o seno de um ângulo assume valores positivos quando sua imagem no ciclo trigonométrico possui ordenada positiva, ou seja, quando essa imagem está acima do eixo Ox, e valores negativos, caso contrário.
Do mesmo modo, o cosseno de um ângulo assume valores positivos quando sua imagem no ciclo trigonométrico possui abscissa positiva, ou seja, quando essa imagem está à direita do eixo OY, valores negativos, caso contrário. Observe que a definição acima coerente com a que foi estabelecida nos triângulos retângulos para ângulos agudos. Basta observar que o triângulo retângulo OPXP possui hipotenusa 1 (raio do ciclo trigonométrico) e catetos |OPx| e |OPy|. Assim, temos: senθ =P̲P̲x/O̲P̲ = O̲P̲y/1 = O̲P̲y e cosθ = O̲P̲/O̲P̲ = O̲P̲x/1 =O̲P̲x.
Denomina-se função seno, a função de ℝ em ℝ definida por f(x)=senx.
O domínio da função seno é Dsen =ℝ e a imagem Imsen =[-1,1].
Denomina-se função cosseno, a função de ℝ em ℝ definida por f(x)=cosx.
O domínio da função cosseno é Dcos=ℝ e a imagem Imcos=[-1,1].
sen θ ∈ [-1,1],∀θ ∈ ℝ
cos θ ∈ [-1,1], ∀θ ∈ ℝ
Seno e cosseno são funções periódicas de período 2π.
Os sinais das funções seno e cosseno em cada um dos quadrantes estão representados nos diagramas a seguir:




