Seja θ um ângulo tal que θ ≠ π/2 + k · π, k ∈ ℤ, e cuja imagem no ciclo trigonométrico é P. A secante de θ é a medida algébrica do segmento O̲P̲’, onde P’ é a interseção da reta tangente ao ciclo trigonométrico em P com o eixo dos cossenos.
Note que, se θ= π/2 + k · π, k ∈ ℤ, a reta tangente não intersecta o eixo cos cossenos e, portanto, a secante de θ não está definida.
Seja θ um ângulo tal que θ ≠ k · π, k ∈ ℤ, e cuja imagem no ciclo trigonométrico é P. A cossecante de θ é a medida algébrica do segmento O̲P̲”, onde P” é a interseção da reta tangente ao ciclo trigonométrico em P com o eixo dos senos.
Note que, se θ=k · π, k ∈ ℤ, a reta tangente não intersecta o eixo dos senos e, portanto, a cossecante de θ não está definida. Na figura a seguir, temos:
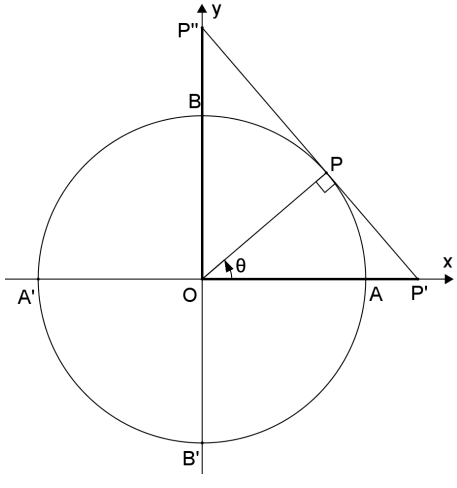
sec θ= O̲P̲’
cossec θ= O̲P̲”
Observe que a definição acima é coerente com a que foi estabelecida nos triângulos retângulos para ângulos agudos. Basta notar que:
ΔOP’: cos θ = OP/OP’ = 1/OP’ ⇔ OP’ = 1/cosθ ⇔ sec θ = OP’
ΔOP”: sen θ = OP/OP” = 1/OP’‘ ⇔ OP” =1/senθ ⇔ cossec θ = OP”
Denomina-se função secante, a função de Dsec em ℝ definida por f(x)=secx.
O domínio da função secante é Dsec = {x ∈ ℝ ∣ x ≠ π/2 + kπ, k ∈ ℤ e a imagem Imcossec =]-∞,-1] ∪ [1,+ ∞ [=ℝ-]-1,1[.
Denomina-se função cossecante, a função de Dcossec em ℝ definida por f(x)=cossecx.
O domínio da função cossecante é Dcossec ={x ∈ ℝ ∣ x ≠ kπ,k ∈ ℤ} e a imagem Imcossec =]-∞,-1] ∪ [1,+∞[=ℝ-]-1,1[.
Secante e cossecante são funções periódicas de período 2π.
Os sinais da secante e da cossecante acompanham os sinais do cosseno e do seno, respectivamente.




