O ciclo trigonométrico é uma circunferência orientada de raio unitário e centrada na origem. A origem do sistema de medidas é no ponto de coordenadas A(1,0) e o sentido positivo é o sentido anti-horário.
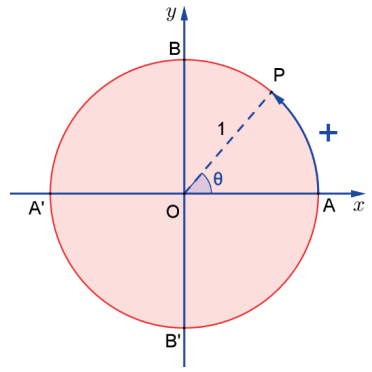
A medida dos ângulos é feita por meio de uma função dos números reais sobre a circunferência, que associa a cada número real θ um único ponto P sobre a circunferência. O ponto P associado ao número real θ é o ponto final de um percurso de comprimento θ sobre a circunferência, a partir de A, no sentido anti-horário para θ >0 ou no sentido horário para θ<0. O Ponto P associado ao número real θ é chamado imagem de θ no ciclo trigonométrico.
Isso é como se você enrolasse a reta real na circunferência com o zero sobre o ponto A e o sentido positivo no sentido anti-horário.
Observe que o ciclo trigonométrico tem comprimento 2π – 1 = 2π. Assim, os arcos pertencentes ao intervalo [0,2π] estão na primeira volta; os arcos pertencentes ao intervalo [2π,4π] estão na segunda volta; os arcos pertencentes ao intervalo [-2π,0] estão na volta -1 ; e assim por diante.
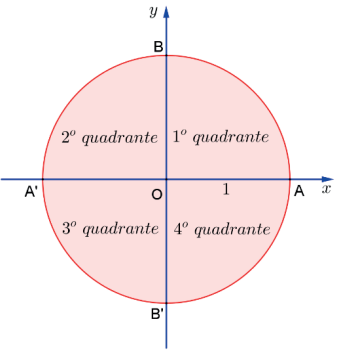
O ciclo trigonométrico é divido em 4 quadrantes de π/2 radianos enumerados no sentido anti-horário. Assim, arcos cujas extremidades estão sobre o arco A̲B̲^ estão no primeiro quadrante (Q); sobre o arco B̲A̲^, no segundo quadrante (QII); sobre o arco B̲A̲’^, no terceiro quadrante (QIII) e sobre o arco B̲’A̲^, no quarto quadrante (QIV).
Para arcos no intervalo [0,2π[ (primeira volta), os arcos do primeiro quadrante pertencem ao intervalo ]0, π/2[, os arcos do segundo quadrante pertencem ao intervalo ]π/2 ,π[, os arcos do terceiro quadrante pertencem ao intervalo ]π, 3π/2[ e os arcos do quarto quadrante pertencem ao intervalo ]3π/2, 2π[.
A figura a seguir traz a indicação dos quadrantes no ciclo trigonométrico.
Exemplo:
Identifique a que quadrante pertence cada um dos arcos a seguir:

Resolução:





