Trigonometria no triângulo (retângulo e qualquer)

TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO

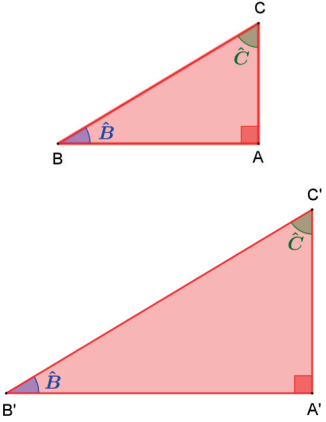
Considere os dois triângulos retângulos ABC e A’B’C’, então podemos escrever 

Se conhecermos a medida dos lados do ∆ABC e de um dos lados do ΔA’B’C’, então é possível calcular seus outros dois lados.

Observe que todos esses dois triângulos possuem a mesma “forma”, diferindo apenas pelo “tamanho”.

Para qualquer triângulo retângulo semelhante ao ∆ABC, é sempre possível, conhecendo-se um dos lados, calcular os outros dois.

A ideia da definição das linhas trigonométricas no triângulo retângulo é identificar características do ∆ABC que permitam calcular os lados dos triângulos retângulos semelhantes a ele sem precisar de um “triângulo matriz”. Para isso vamos lançar mão de uma característica que todos esses triângulos semelhantes têm em comum. Eles possuem os mesmos ângulos.

Assim, para todos os triângulos retângulos semelhantes ao ∆ABC, a razão entre o cateto oposto ao ângulo B^ e a hipotenusa é a mesma. A essa razão damos o nome de seno de B^{^}. Da mesma forma, a razão entre o cateto adjacente ao ângulo B^{^} e a hipotenusa é constante. A essa razão damos o nome de cosseno de B^. A razão entre o cateto oposto e o cateto adjacente ao ângulo B^{^} é chamada de tangente de B^{^}.

Seja o triângulo ABC retângulo em A, conforme a figura a seguir: 

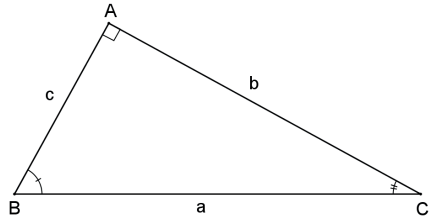
Definem-se, para o ângulo agudo B^{^}.

LEI DOS SENOS

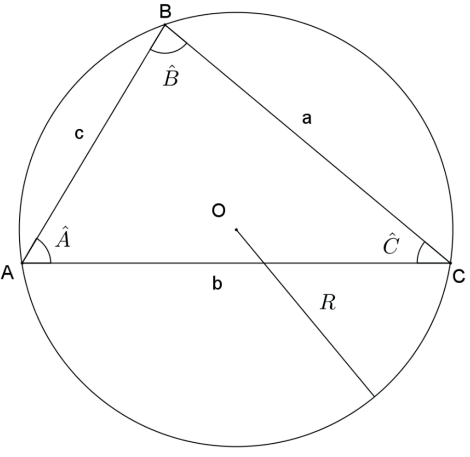
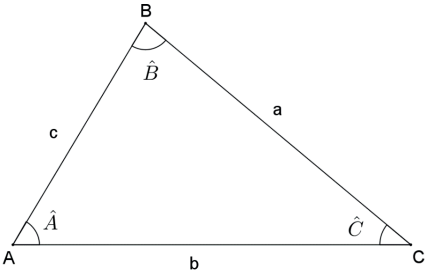
Seja um triângulo ABC de lados BC¯=a, AC¯=be AB¯=c e raio do círculo circunscrito R, então

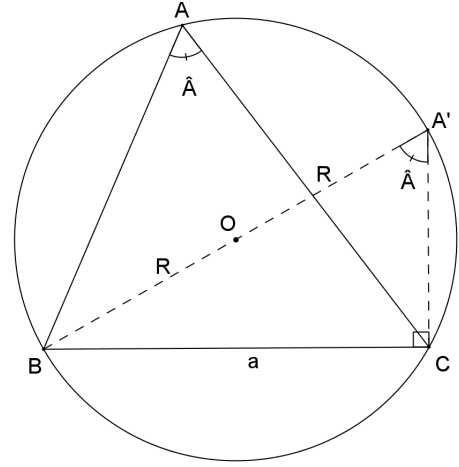
Demonstração:

Adotando procedimento análogo para os outros vértices, temos 

LEI DOS COSSENOS

Seja um triângulo ABC de lados BC¯=a, BC¯=a e AC¯=b, então

Demonstração:

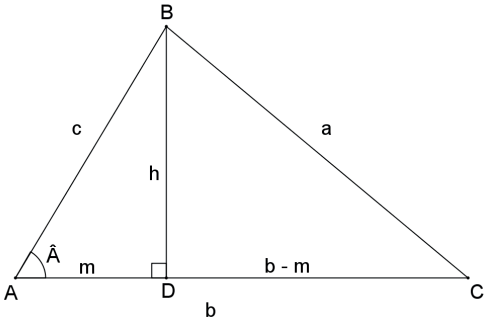
Aplicando o teorema de Pitágoras no triângulo retângulo ABD, temos: m² + h² =c².

Aplicando o teorema de Pitágoras no triângulo retângulo BCD, temos: (b – m)² + h² = a².

No triângulo retângulo ABD, temos: cosA= ^m/_c ⇔ m = c · cosA.

⇒ b² – 2bm + c² = a² ⇔ a² = b² + c² – 2bccosA (C.Q.D.)