Assim, dois arcos α e β, expressos em radianos, são côngruos (α≡β) se, e somente se, α-β = 2π·k para algum k ∈ ℤ.
Da mesma forma, dois arcos α e β, expressos em graus, são côngruos (α≡β) se, e somente se, α-β = 360° · k para algum k ∈ ℤ.
α ≡ β ⇔ α – β = 2k · π, k ∈ ℤ (radianos)
α ≡ β ⇔ α – β= 360°· π, k ∈ ℤ (graus)
Exemplo:
Marque no ciclo trigonométrico a imagem de cada um dos números a seguir e identifique os arcos côngruos.
a) 7π/3
b) 19π/4
c) – 5π/4
d) – 11π/4
e) – 5π/3
f) 14π/3
Resolução:
a) 7π/3 = π/3 + 6π/3 = π/3 + 2π
b) 19π/4 = 3π+16π/4 = 3π/4 +2π·2
c) – 5π/4 = 3π-8π/4 = 3π/4 +2π · (-1)
d)- 11π/4 = 5π-16π/4 = 5π/4 +2π · (-2)
e) – 5π/3 = π-6π/3 = π/3 + 2π · (-1)
f) 14π/3 = 2π + 12π/3 = 2π/3 + 2π . 2
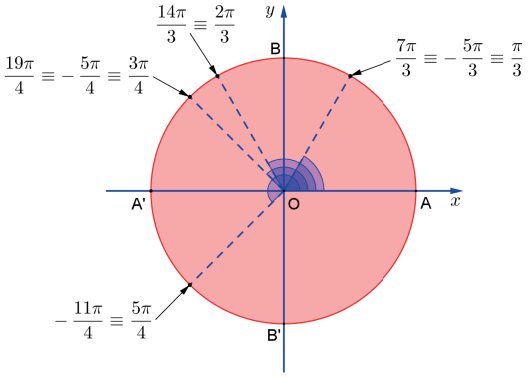
Os arcos das opções a) e e) são côngruos, assim como os das opções b) e c).
A primeira determinação positiva de um arco β é o arco α ∈ [0,2π[ côngruo a β.
Para se identificar a imagem de um arco no ciclo trigonométrico e os valores de suas linhas trigonométricas é sempre útil encontrar a primeira determinação positiva.
Exemplo:
Encontre a primeira determinação positiva dos seguintes arcos.
a) 35π/4
b) 25π/6
c) – 40π/3
d) 2880°
e) -1200°
Resolução:
a) A primeira determinação positiva de 35π/4 é 3π/4, pois 35π/4= 32π+ 3π/4 = 3π/4 + 2π· 4.
b) A primeira determinação positiva de 25π/6 é π/6, pois 25π/6 = π+24π/6 = π/6 + 2π · 2.
c) A primeira determinação positiva de – 40π/3 é 2π/3, pois – 40π/3 =-42π+2π/3 =2π/3 + 2π · (-7).
d) A primeira determinação positiva de 2730° é 210°, pois 2730° = 360° · 7 + 210°.
e) A primeira determinação positiva de -1200° é 240º, pois -1200° = 360° · (-4) + 240°.




