ÂNGULOS DE 30° E 60°
Seja o triângulo equilátero ABC de lado x, conforme a figura a seguir:
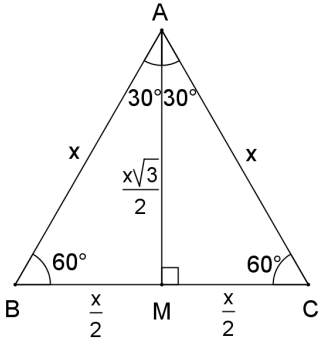
Seja M o ponto médio do lado B̲C̲, então AMB=90°. Aplicando o teorema de Pitágoras no triângulo retângulo AMB, temos:
A̲M̲² +B̲M̲² = B̲M̲² ⇔ A̲M̲² + (x/2)² = x2 ⇔ A̲M̲² =x² – x²/4 = 3x²/4 ⇔ A̲M̲= x√3/2
No triângulo retângulo AMB, temos:
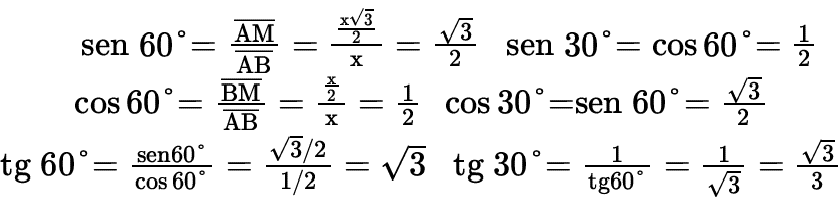
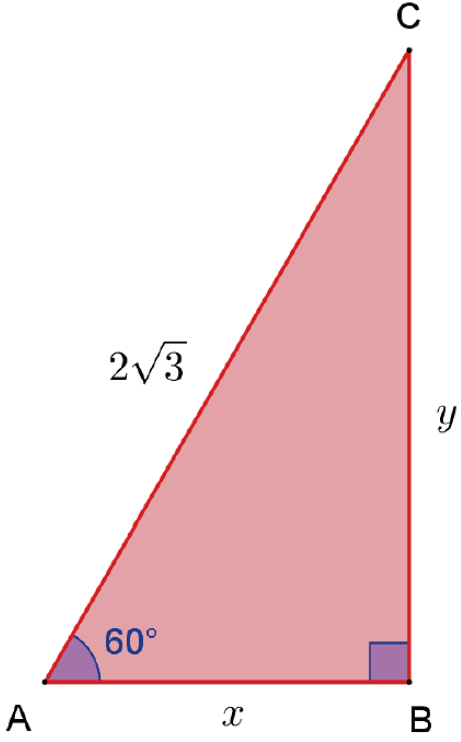
Exemplo: calcule x e y na figura.
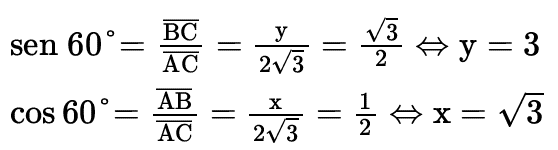
ÂNGULO DE 45°
Seja o quadrado ABCD de lado x, conforme a figura a seguir:
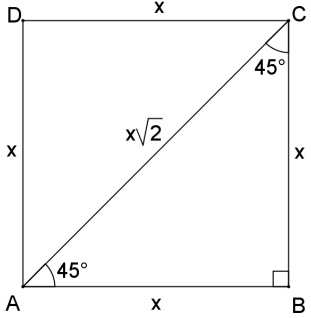
Aplicando o teorema de Pitágoras no triângulo retângulo ABC, temos:
A̲C̲² = A̲B̲² + B̲C̲² ⇒ A̲C̲²= x²+ x² = 2x² ⇔ A̲C̲= x√2.
No triângulo retângulo ABC, temos:
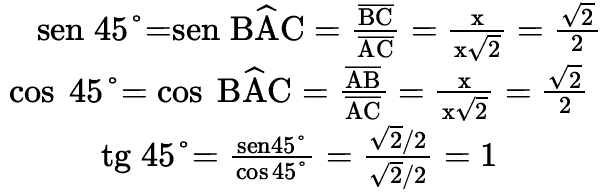
Note que sen 45° =cos (90°-45°)= cos 45°.
Exemplo:
Calcule os catetos de um triângulo retângulo isósceles de hipotenusa 4.
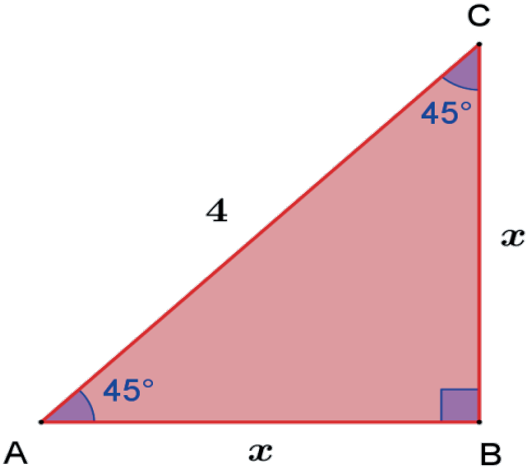
sen = 45° = B̲C̲/A̲C̲ = x/4 = √2/2 ⇔ x = 2 √2
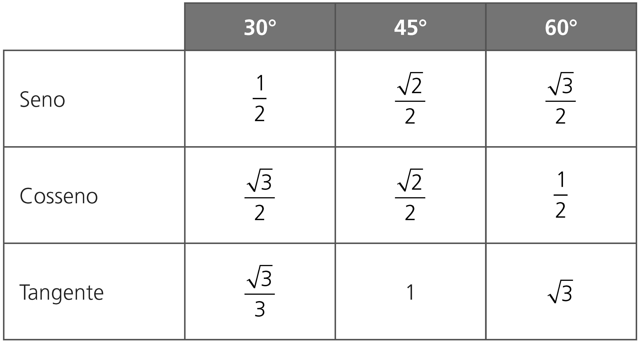
Quadro resumo: