TRANSMUTAÇÕES NATURAIS OU DECAIMENTOS RADIOATIVOS
As emissões Alfa e Beta, quando emitidas, são capazes de alterar o número atômico do núcleo emissor, isso acarreta na alteração química na amostra, já que o novo núcleo obtido passa a pertencer a outro elemento químico. Qualquer emissão que apresenta essa propriedade é denominada de “emissão transmutável “.
A emissão gama não apresenta essa propriedade.
Emissão Alfa (Lei de Soddy)
“Quando um radioisótopo emite uma partícula alfa (α), o seu número atômico se reduz de duas unidades e seu número de massa se reduz de quatro unidades.”
Exemplo:

Emissão Beta (Lei de Soddy – Fajans – Russel)
“Quando um radioisótopo emite uma partícula beta (β) o seu número atômico aumenta de uma unidade e seu número de massa permanece constante.”
Exemplo:

Exercícios resolvidos
01. Determine o número de partículas alfa (α) e beta (β) emitidas na transformação do urânio –235 em chumbo –207.
Resolução:
Podemos escrever a seguinte equação genérica:

A quantidade de partículas iniciais deve ser igual a quantidade de partículas finais, desse forma podemos igualar, respectivamente, os números de massas e os números atômicos.
Números de massas:
4x = 235–207→
→ 235 = (x)(4) + (y)(0) + 207→
→ 4x + 28→
→ x = 7
α → 7α
Números atômicos:
92 = (2)(x) + (–1)(y) + 82→
→ 92 = (2)(7) – y + 82→
→ y = 82 + 14 – 92 = 4→
β → 4β
02. Um radioisótopo X, ao emitir 3 partículas alfa e 5 partículas beta, transformou-se no isótopo do elemento rádio de número de massa 226.
a) Identifique o elemento X consultando a Classificação Periódica dos elementos.
b) Determine o número de nêutrons do elemento X.
Resolução:
a) Chamamos de “a” e “b” o número atômico e o número de massa de X, respectivamente.
Escrevemos então, a equação:

A quantidade de partículas iniciais deve ser igual a quantidade de partículas finais, dessa forma podemos igualar, respectivamente, os números de massas e os números atômicos.
Números de massas:
b = (3)(4) + (5)(0) + 226→
b = 12 + 226 = 238
Números atômicos:
a = (3)(2) + (-1)(5) + 88 → a = 6 – 5 + 88 = 89 → Actínio (Ac)
b) A = Z + n → 238 = 89 + n → n = 149 nêutrons.
TRANSMUTAÇÕES ARTIFICIAIS
TRANSMUTAÇÃO DE RUTHERFORD

Observação: mesmo conservando o número de total de partículas, essas reações não estão de acordo com a Lei de Lavoisier. A explicação para esse fenômeno se dá pelo fato de que reações em que as partículas se deslocam em velocidades próximas a da luz apresentam transformação de um pequeno fragmento de sua massa em uma grande quantidade de energia liberada principalmente na forma de calor. O cálculo da quantidade de energia obtida numa transformação dessa natureza, pode ser dada pela Equação de Einstein:
E = ∆mc2, onde:
∆m → a variação de massa.
c → velocidade da luz no vácuo. (3 × 108 ms-1)
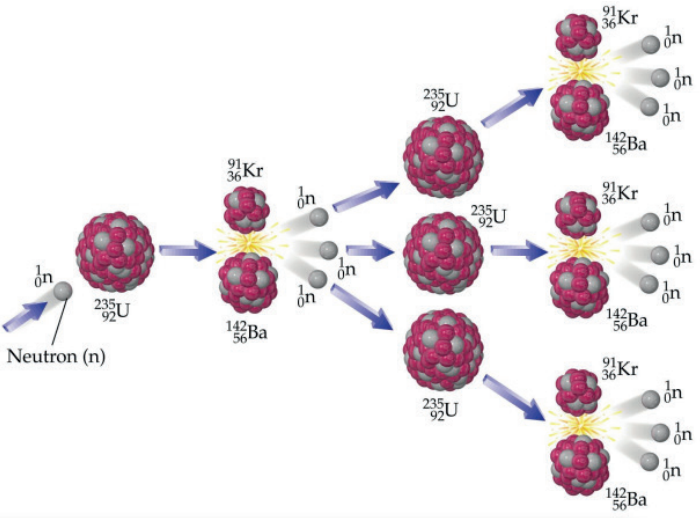
FISSÃO NUCLEAR

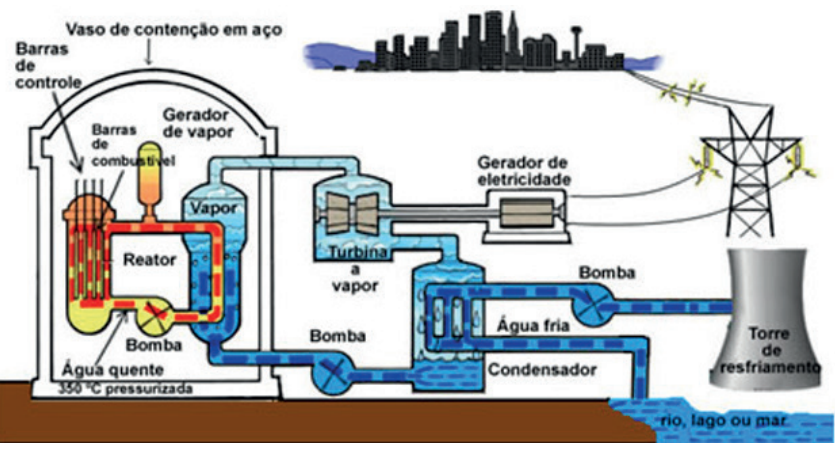
REATOR NUCLEAR
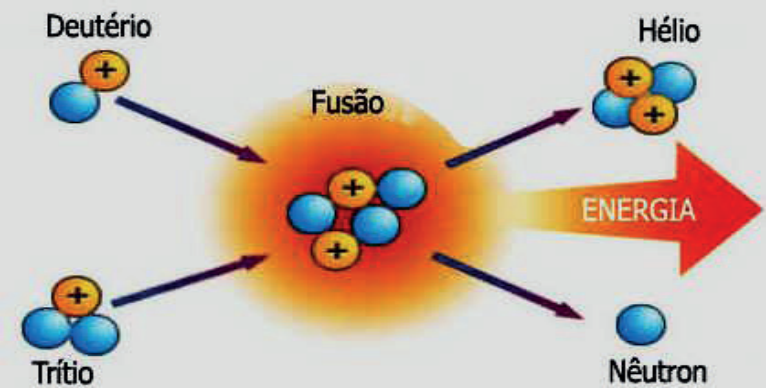
FUSÃO NUCLEAR

Exemplo: consultando a classificação periódica dos elementos, identifique os nuclídeos x, y e z que completam as respectivas equações nucleares.

Resolução: para todos os casos, devemos usar a conservação do número total de partículas. Chamamos de “a” e “b” o número atômico e o número de massa de cada partícula desconhecida, respectivamente, podemos efetuar os cálculos da seguinte forma:
a) Números de massas:
11 + 4 = 14 +b → b = 15 – 14 = 1
Números atômicos:
4 + 2 = 6 + a → a = 6 – 6 = 0 → 0x1 → 0 n1 (nêutron)
b) Números de massas:
210 + (2)(1) = b + (4)(1) → b = 210 + 2 – 4 = 206
Número atômicos:
84 + (2)(0) = a + (4)(1) → a = 84 – 4 = 80 → 80Hg206 (mercúrio)
c) Números de massas:
23 + 11 = b + (3)(0) → b = 23 + 11 = 44
Números atômicos:





