Tipos especiais de matrizes

MATRIZ QUADRADA

A matriz constituída pelo mesmo número de linhas e colunas é chamada matriz quadrada.

Assim, uma matriz constituída por n linhas e n colunas é uma matriz quadrada de ordem n × n ou simplesmente uma matriz quadrada de ordem n.

MATRIZ NULA 

É toda matriz que possui todos os seus elementos iguais a zero.

A matriz nula é o elemento neutro da adição de matrizes, assim A + 0 =A e 0 + A = A.

MATRIZ DIAGONAL

É toda matriz quadrada em que os elementos não pertencentes à diagonal principal são iguais a zero, ou seja, a_ij = 0 sempre que i ≠ j.

MATRIZ IDENTIDADE

É a matriz diagonal, na qual todos os elementos da diagonal principal são iguais a 1.

A matriz identidade é o elemento neutro da multiplicação de matrizes, assim A_m×n · I_n = Im · A_m×n – A_m×n.

MATRIZ TRIANGULAR SUPERIOR

Chama-se matriz triangular superior a matriz quadrada que possui todos os elementos abaixo da diagonal principal nulos.

A é triangular superior ⇒ a_ij = 0, se i > j

MATRIZ TRIANGULAR INFERIOR

Chama-se matriz triangular inferior a matriz quadrada que possui todos os elementos abaixo da diagonal principal nulos.

A é triangular inferior ⇒ a_ij =0, se i < j.

MATRIZ TRANSPOSTA

A matriz transposta de A,At, é a matriz obtida a partir de A, trocando-se ordenadamente suas linhas por colunas.

Seja A = (aij)_m×n então A^t = (bij)_m×n , onde b_ij = a_ij para todo i, j.

A matriz transposta de A possui tantas linhas quantas são as colunas e tantas linhas quantas são as colunas de A.

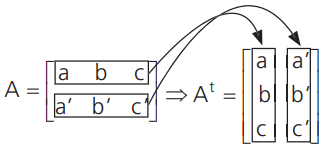
A transposta de uma matriz quadrada pode ser obtida invertendo os elementos em relação à diagonal principal. Os elementos da diagonal principal não mudam de posição.

PROPRIEDADES

a. (A^t)^t = A

b. (A + B)^t = A^t + B^t

c. (A – B)^t = A^t – B^t

d. k ∈ R ⇒ (kA)^t = k · A^t

e. (A · B)^t = B^t · A^t

f. (A · B · C)^t = C^t · B^t · A^t

MATRIZ SIMÉTRICA

Uma matriz quadrada diz-se simétrica quando a_ij = a_ji para todo 1 ≤ i, j ≤ n, ou seja, quando é igual à sua matriz transposta.

Daí resulta que os elementos simétricos em relação à diagonal principal são iguais.

A é simétrica ⇒ A = A^t

MATRIZ ANTISSIMÉTRICA

Uma matriz quadrada diz-se antissimétrica quando a_ij = -a_ji para todo 1 ≤ i, j ≤ n, ou seja, quando é igual à oposta de sua matriz transposta.

A é antissimétrica ⇒ A = -A^t

Daí resulta que os elementos simétricos em relação à diagonal principal são opostos e os elementos pertencentes à diagonal principal são nulos.