FUNÇÕES MONOTÔNICAS
Chama-se monotônica ou monótona a função que é sempre crescente ou decrescente no seu domínio.
Seja a função f : A → B, então:
- f é crescente (não decrescente) se ∀x, y ∈ A tais que x < y ⇒ f(x) < f(y).
- f é decrescente (não crescente) se ∀x,y ∈ A tais que x < y ⇒ f(x) > f(y).
- f é estritamente crescente (crescente) se ∀x, y ∈ A tais que x < y ⇒ f(x) < f(y).
- f é estritamente decrescente (decrescente) se ∀x, y ∈ A tais que x < y ⇒ f(x) > f(y).
São funções crescentes f(x) = 3x – 1, f(x) = 2x e f(x) = x3.
São funções decrescentes f(x) = -2x + 5, f(x) = (1/2)x e f(x) = -x3.
As funções f(x) = x2 e f(x) = sen x não são crescentes e nem decrescentes em i.
Esses conceitos são facilmente observados no gráfico da função. Nas funçōes crescentes o gráfico “sobe” para a direita, enquanto nas funçōes decrescentes o gráfico “desce” para a direita.
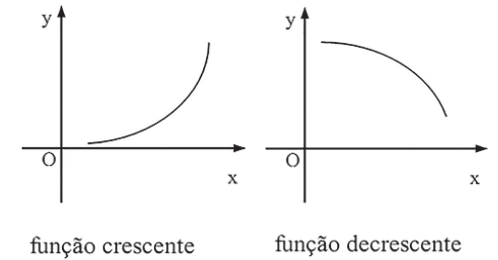
Já a função a seguir não é monótona, pois ela é decrescente numa parte do domínio e crescente em outra.
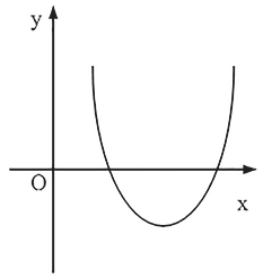
PARIDADE
FUNÇÃO PAR
Seja A um conjunto tal que x ∈ A ⇒ – x ∈ A e a função f : A → B. Diz-se que:
f é par ⇔ f(x) = f(-x), ∀ x ∈ A
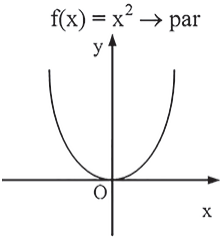
Exemplo: f(x) = x2 e f(x) = cos x.
O gráfico das funções pares é simétrico em relação ao eixo Oy, pois (x, y) ∈ f⇔ (-x, y) ∈ f.
FUNÇÃO ÍMPAR
Seja A um conjunto tal que x ∈ A ⇒ -x ∈ A e a função f : A → B. Diz-se que:
f é impar ⇔ f(-x) = -f(x), ∀ x ∈ A
Exemplo: f(x) = x3 e f(x) = sen x
O gráfico das funções ímpares é simétrico em relação a origem, pois (x,y) ∈ f ⇔ (-x,-y) ∈ f.
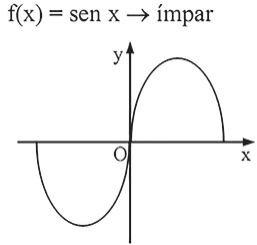
Se uma função não é nem par nem ímpar dizemos que ela não possui paridade.
Exemplo: f(x) = x2 + x – 1.
Para identificar a paridade de uma função devemos obter a expressão de f(-x). Caso essa expressão seja idêntica à de f(x), a função é par, caso seja idêntica à de -f(x), a função é ímpar, e caso não seja idêntica a nenhuma das duas, a função não possui paridade.
Note que devemos obter identidades, não basta que a igualdade ocorra para alguns pontos, ele tem que ocorrer em todo o domínio.
Exemplo: identifique a paridade de f(x) = x5 + sen3x.
f(-x) = (-x)5 + sen3(-x) = -x5 + (-senx)3 = -x5 – sen3x = -f(x), ∀ x ∈ ℝ
Logo, a função é ímpar.
ProBizu: a soma, diferença, produto ou quociente de duas funções pares é uma função par. A soma ou diferença de duas funções ímpares é uma função ímpar. O produto ou o quociente de duas funçōes ímpares é função par.
TIPOLOGIA DAS FUNÇÕES
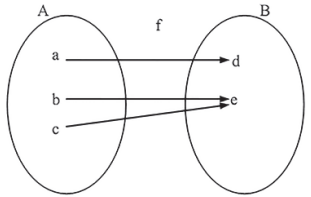
A função f : A → B é sobrejetora quando todo elemento de B está associado por f a pelo menos um elemento de A, ou seja, quando a imagem da função é igual ao seu contradomínio.
f : A → B é sobrejetora ⇔ ∀y ∈ B, ∃x ∈ A tal que (x, y) ∈ f ou y = f(x).
No diagrama de flechas, todo elemento do contradomínio B recebe flecha.
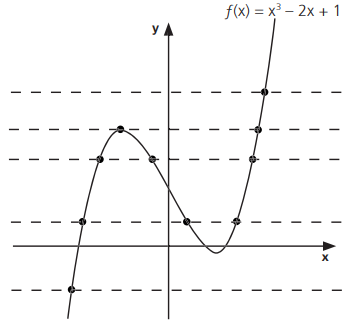
No gráfico, retas horizontais traçadas a partir de pontos do contradomínio intersectam o gráfico em pelo menos um ponto.
Exemplo: a função f : ℝ → ℝ dada por f(x) = x3 – 2x + 1 é sobrejetora, mas não é injetora. Observe que as retas horizontais traçadas intersectam o gráfico em um, dois ou três pontos.
A função f : A → B é injetora quando cada elemento de B está associado por f a no máximo um elemento de A, ou seja, elementos distintos de A estão associados a elementos distintos de B.

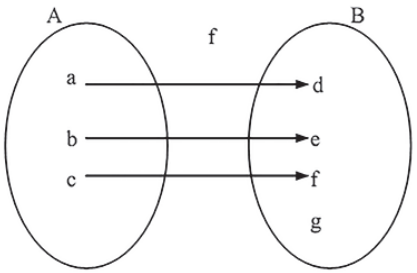
No gráfico, retas horizontais traçadas a partir de pontos do contradomínio intersectam o gráfico em no máximo um ponto.
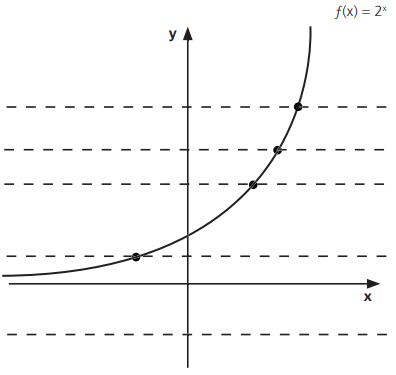
Exemplo: a função f : ℝ → ℝ dada por f(x) = 2x é injetora, mas não é sobrejetora. Observe que as retas horizontais traçadas intersectam o gráfico em um ou nenhum ponto.
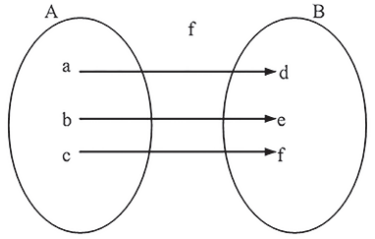
A função f : A → B é bijetora se, e somente se, é sobrejetora e injetora, ou seja, todo elemento de B está associado por f a um único elemento de A.
No diagrama de flechas, todo elemento de B recebe exatamente uma flecha.
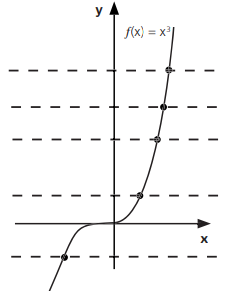
No gráfico, retas horizontais traçadas a partir de pontos do contradomínio intersectam o gráfico em exatamente um ponto.
Exemplo: a função f : ℝ → ℝ dada por f(x) = x3 é bijetora. Observe que as retas horizontais traçadas intersectam o gráfico em exatamente um ponto.
ProBiz: seja f : A → B, onde A e B são conjuntos finitos e suas quantidades de elementos são dadas por #(A) e #(B), respectivamente, então
se f é sobrejetora, então (A) ≥ (B);
se f é injetora, então (A) ≤ (B); e
se f é bijetora, então (A) = (B).
FUNÇÃO LIMITADA
Uma função f é limitada se ∃K > 0 tal que ∀x ∈ Df ⇒ |f(x)| < K.
Exemplo:
A função f(x) = sen x é uma função limitada, pois ∀x ∈ ℝ, temos -1 ≤ senx ≤ 1 ⇔ |senx| ≤ 1.
A função f(x) = x2 não é limitada, pois ∀K > 0,∃x ∈ Df tal que f(x) = x2 > K.
FUNÇÃO PERIÓDICA
Uma função f é periódica se, e somente se, ∃p > 0 tal que f(x) = f(x + p),∀x ∈ Df.
Isso significa que os valores da função se repetem em intervalos de tamanho p > 0. O menor número positivo p com essa propriedade é chamado período da função.
Os exemplos mais comuns de funções periódicas são as funções trigonométricas. A função f(x) = sen x, por exemplo, é uma função periódica de período 2π, pois sen (x + 2π) = sen x,∀x ∈ ℝ.




