Termodinâmica: Entalpia (H)

ENTALPIA(H)

Numa transformação isobárica, como se processa a maioria das reações químicas e numa dada temperatura, podemos escrever a equação do Primeiro Princípio da Termodinâmica da seguinte forma:

U = Q − W → ΔU = Q_p − PΔV, onde Q_p é a quantidade de calor à pressão constante.

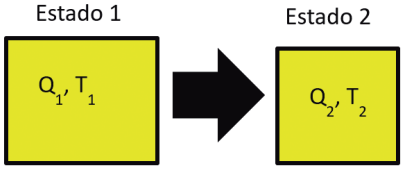
Considerando que sistema se modificou de uma situação 1 para uma outra situação 2, temos:

ΔU = Q_p − PΔV
U₂ − U₁ = Qp − P(V₂ − V₁)
U₂ − U₁ = Q_P − PV₂ + PV₁

Arrumando os termos, temos:

(U₂ + PV₂) − (U₁ + PV₁) = Q_P

Características do termo U + PV

I. É um conteúdo energético (calorífico). 
II. Como é função de três funções de estado, é também uma função de estado.
III. A esse conteúdo energético será denominado de Entalpia (H).

Podemos então escrever a equação:

(U₂ + PV₂) − (U₁ + PV₁) = Q_p → H₂ − H₁ = Q_P
ΔH = Q_p

A equação H = U + PV, que define a Entalpia, pode também receber um tratamento diferencial:

H = U + PV → ΔH = ΔU + (PΔV + VΔP) → como a transformação é isobárica (∆P = 0), temos:

ΔH = ΔU + PΔV → ΔU = ΔH − PΔV → Equação do Primeiro Princípio da Termodinâmica numa transformação isobárica.

Numa reação química em que estão presentes componentes gasosos, a variação de volume e, consequentemente, a realização de trabalho, é causada pela variação do número de mols. Podemos então utilizar a Equação de Clapeyron da seguinte forma:

PV = n ⋅ R ⋅ T → PΔV = ΔnRT, o que nos leva a escrever: ΔH = ΔU + ΔnRT

CAPACIDADE CALORÍFICA (C)

Estuda a variação quantidade de calor em função da variação da variação de temperatura.

Observação: Costumamos trabalhar com dois tipos de capacidade calorífica, o C_v, a capacidade calorífica à volume constante, numa transformação isocórica e C_p, a capacidade calorífica à pressão constante, numa transformação isobárica.

Podemos escrever as seguintes equações:

Se U = Q − W → dU = dQ − pdV − vdP

No caso de uma transformação isocórica temos: dU = dQ − vdP(1)

Como U é uma função de estado podemos escrever U=f(T, V).

Como as equações (1) e (2) descrevem a mesma grandeza, energia interna, podemos afirmar que o primeiro da equação 2 descreve a variação da quantidade de calor com a temperatura numa transformação à volume constante, C_v. Desse modo, podemos chegar a seguinte equação:

No caso de uma transformação isobárica temos:

dH = dU − PdV   (1)

Como H é uma função de estado podemos escrever H=f(T, P):

Como as equações (1) e (2) descrevem a mesma grandeza, energia interna, podemos afirmar que o primeiro da equação 2 descreve a variação da quantidade de calor com a temperatura numa transformação à pressão constante, C_p. Desse modo, podemos chegar a seguinte equação:

dH = C_pdT

Exemplo:

Determine a temperatura máxima, em ºC, que uma chama que queima consumindo 1,6 Kg de butano (C₄H₁₀) com quantidade estequiométrica de ar atmosférico que foi inicialmente acionada a 25º C.

Dados:

Massas Atômicas: H=1; C=12; N=14; O=16
Composição volumétrica do ar: 80% de Nitrogênio e 20% de Oxigênio.
Entalpias combustão do butano = -2878 kJ⋅mol-1.
Capacidades caloríficas à pressão constante:

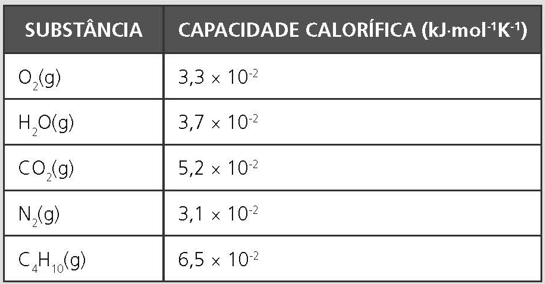
Resolução:

Equação Química de Combustão

Para 1 mol de C₄H₁₀ sem a presença de N₂:

Para 1 mol de C₄H₁₀ com a presença de N₂:

Para 20 mol de C₄H₁₀ com a presença de N₂:

Quantidade de calor produzido → Q = (20)(2878) = 57560 KJ

Essa quantidade de calor aquece os gases presentes nos produtos formados. Então:

CLASSIFICAÇÃO DAS TRANFORMAÇÕES DO PONTO DE VISTA TERMOQUÍMICO

VARIAÇÃO DE ENTALPIA (∆H)

Por se tratar de uma função de estado, a entalpia não é uma grandeza absoluta, logo esta precisa ser medida entre dois pontos (instantes) da transformação analisada. Sendo assim é comum falarmos de variação de entalpia. Quando nos referimos à algum valor de entalpia pontual, é porque foi arbitrariamente escolhido um valor que servirá como referencial.

ΔH = H_{(estado final)} − H_{(estado inicial)}

I. CÁLCULO DO ∆H DE UMA DADA TRANSFORMAÇÃO

Considere a transformação representada pela equação abaixo:

(x)A + (y)B → (z)C + (w)D, onde x, y, z e w representam os coeficientes (número de mols) de cada espécie participante da transformação.

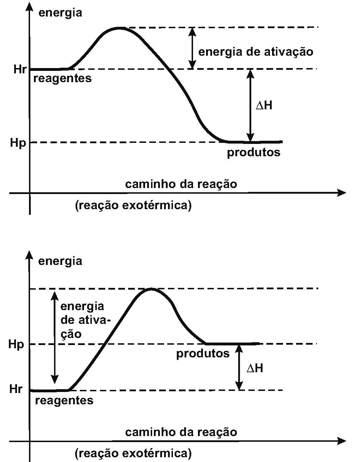
EAÇÕES (OU TRANSFORMAÇÕES) ENDOTÉRMICAS

REAÇÕES (OU TRANSFORMAÇÕES) EXOTÉRMICAS

I. ENERGIA DE ATIVAÇÃO (E_AT)

É uma quantidade de energia absorvida pelas moléculas dos reagentes necessária para promover a quebra de ligações químicas que originará a formação das moléculas dos produtos.

Exemplo:

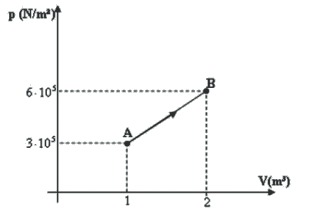
01. O gráfico abaixo ilustra uma transformação 100 mols de gás ideal monoatômico recebem do meio exterior uma quantidade de calor 18 · 10⁵ J.

Dado: R = 8  J/mol⋅K.

Determine:

a) o trabalho realizado pelo gás;
b) a variação da energia interna do gás;
c) a temperatura do gás no estado A.

Resolução:

a) O trabalho realizado pode ser calculado pela área do gráfico:

b) U − Q − W → U = 18 · 10⁵ − 4,5 · 10⁵ = 13,5 · 10⁵J ou  13,5 · 10⁵J/100 mol = 13,5 · 10³J ⋅ mol⁻¹ = 13,5 KJ ⋅ mol⁻¹

c) PV = nRT → no ponto A → (3 · 10⁵Nm⁻²) · (1m³) = (100 mol) → T = 37,5 K

02. Considere a reação de combustão completa do propano, a º1 atm e 27º C, representada pela reação química abaixo:

C₃H_8(g) + 5O_2(g) → 3CO_2(g) + 4H₂O_(ℓ)

ΔH =−2220 KJ · mol⁻¹

Para um consumo de 2,2 Kg de propano, determine:

O trabalho realizado em KJ.
A energia interna em KJ.

Dado: Massas Atômicas: H = 1; C = 12; R = 8 J/mol⋅K.

Resolução:

a) W = ΔnRT

b) ΔU = ΔH − W → ΔU(1mol de C₃H₈) = (−2220000)−(2400)=2222400 J=2.222,4 KJ ⋅ mol⁻¹

ΔU = (50) ⋅ (2222,4) = 111 ⋅ 120 KJ

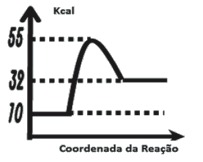
03. Considere os diagramas abaixo:

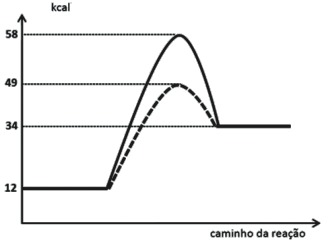
a) Para a reação I, calcule o valor da variação de entalpia e da energia de ativação.

b) Para a reação II, calcule os valores da energia de ativação na ausência e na presença de catalisador.

Resolução:

Observando os gráficos: