PRIMEIRO TEOREMA
O primeiro teorema define que a área de uma superfície de revolução é igual ao produto do comprimento da curva geratriz pelo comprimento do caminho percorrido pelo centroide (centro de massa) dessa mesma curva ao longo do ângulo que gera a superfície.
Ou seja, o comprimento do caminho percorrido pelo centroide é o comprimento de circunferência, assim 2π multiplicado pelo raio, que nesse caso é a distância do centro de massa ao eixo de rotação.
Assim S = 2πdL, sendo L o comprimento da curva.
SEGUNDO TEOREMA
O segundo teorema define que o volume de um sólido de revolução é igual ao produto da área da superfície geratriz pelo comprimento do caminho percorrido pelo centroide dessa mesma superfície ao longo do ângulo que gera o volume.
Sendo A a área que será rotacionada, teremos de maneira análoga ao primeiro teorema V = 2πdA.
Exemplo:
Vamos imaginar a figura abaixo sendo rotacionada em relação ao eixo de rotação destacado.
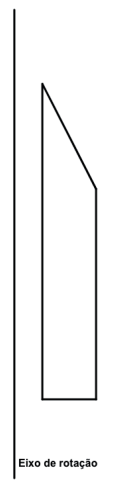
Ao rotacionarmos teremos a formação do seguinte sólido.
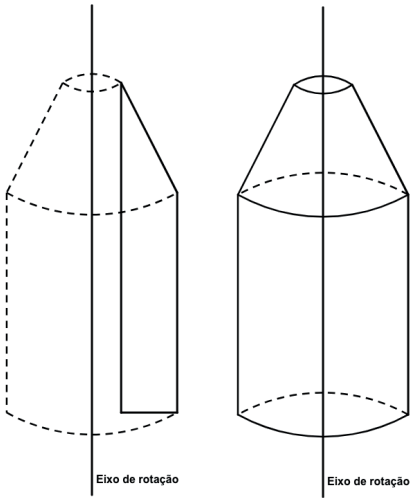
Assim para calcularmos a área e o volume desse sólido teríamos.
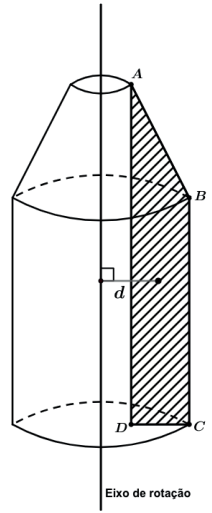
Assim sua área e volume serão

Vamos supor que o lado AD dista 2 cm do eixo de rotação e que AD = 10 cm, BC = 6 cm, e CD = 2 cm.

Para calcularmos AB utilizaremos o teorema de Pitágoras.

Assim





