TEOREMA DE D’ALEMBERT
O resto da divisão de um polinômio P(x) por x − a é igual a P(a).
Seja, com efeito, P(x) = amxm + am−1xm−1+ … + a0, um polinômio de x, ordenado segundo as potências decrescentes de x. Designemos o quociente dessa divisão por Q(x) e o resto por R.
O resto tendo grau inferior ao divisor, que é do primeiro grau, será de grau zero, isto é, independente de x.
Podemos, pois, estabelecer a seguinte identidade:
P(x) = (x − a) ⋅ Q(x) + R
Substituindo nesta identidade x por a, teremos:
P(a) ≡ (a − a) ⋅ Q(a) + R
P(a) ≡ 0 ⋅ Q(a) + R
P(a) = R
Este resultado nos mostra que R é uma constante, isto é, equivale ao valor numérico P(a) de Polinômio P(x), para x = a.
Observação: Quando o polinômio divisor é da forma x + a, devemos substituir no polinômio P(x), x por – a, visto que: x + a = x – (–a).
CONSEQUÊNCIA 1: para que um polinômio em x seja divisível por x − a, é condição necessária e suficiente que ele se anule para x = a.
CONSEQUÊNCIA 2: para que um polinômio em x seja divisível por x + a, é condição necessária e suficiente que ele se anule para x = – a.
Exemplo:
Calcular o resto da divisão (5x4 − 8x3 + 3x2 − 10x + 7) : (x − 2)
Resolução:
R = 5 ⋅ 24 − 8 ⋅ 23 + 3 ⋅ 22 − 10 ⋅ 2 + 7
R = 80 − 64 + 12 − 20 + 7
R = 15
REGRA DE RUFFINI
O quociente da divisão de um polinômio completo e ordenado em relação a x do grau m por um binômio da forma x − a, é um polinômio e, ordenado em relação a x, é do grau m – 1, no qual:
1º. o coeficiente do primeiro termo é o mesmo do primeiro termo do polinômio dividendo;
2º. o coeficiente de cada termo é igual à soma do coeficiente de mesma ordem do dividendo com o coeficiente do termo anterior multiplicado por a;
3º. o resto da divisão é igual à soma do coeficiente do último termo do dividendo com o coeficiente do último termo do quociente multiplicado por a.
Exemplos:
01. Calcular o quociente e o resto da divisão (x3 + 5x2 + x − 1) : (x + 5)
Resolução:
b2 = 1
b1= 1(−5) + 5=0
b0 = 0(−5) + 1=1
R = 1(−5) − 1
Q(x) = x2 + 1 e R=−6
02. Usando o dispositivo prático, dividir 2x3 − 5x2 + 3x − 4 por x−2
Resolução:
Inicialmente alocar no dispositivo os coeficientes do dividendo e o segundo termo do binômio com o sinal trocado e então proceder como acima:

Q(x) = 2x2 − x + 1 e R = −2
Vamos detalhar a seguir o dispositivo.
DISPOSITIVO PRÁTICO DE BRIOTT-RUFFINI
Para dividir um polinômio P(x) = anxn + an−1xn−1 +…+ a2x2 + a1x + a0 por x − a, devemos seguir o seguinte algoritmo:
1º. Na primeira linha do diagrama, dispomos a raiz a do divisor na coluna à esquerda e a seguir os coeficientes de P(x), inclusive os nulos;

2º. Na segunda linha do diagrama, dispomos o coeficiente do primeiro termo do dividendo que será o coeficiente do primeiro termo do quociente;

3º. À direita do termo anterior colocamos a ⋅ qn − 1 + an−1 = qn−2, coeficiente do segundo termo do quociente;
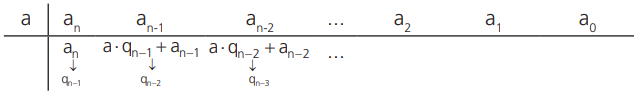
4º. Repete-se a operação descrita no item anterior até atingirmos q0 P(x) = x3 + kx2 + px − 9;
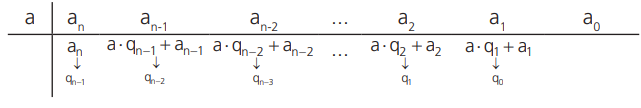
5º. Repetindo o procedimento mais uma vez obtemos o resto r = a ⋅ q0 + a0 da divisão.
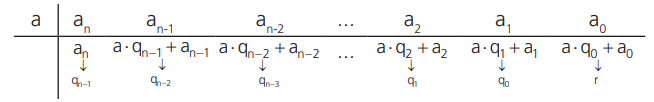
TEOREMA FUNDAMENTAL DA ÁLGEBRA
Todo polinômio de grau maior ou igual a 1 admite pelo menos uma raiz real ou complexa.
TEOREMA DA DECOMPOSIÇÃO
Se o número complexo αα é raiz de um polinômio P, então P(x) é divisível por α(x – α).
Todo polinômio P(x) de grau n ≥ 1 P(x) = anxn + an−1xn−1 +…+ a2x2 + a1x + a0 (an ≠ 0) pode ser decomposto em n fatores do primeiro grau de maneira única, a menos da ordem, como segue:
P(x) = an(x − r1) · (x − r2) ⋅…⋅ (x − rn)
onde r1, r2, …, rn são as raízes (complexas) do polinômio.
TEOREMA:
Um polinômio de grau n possui exatamente n raízes complexas. Desta forma, a quantidade de raízes reais é no máximo igual a n.
CONGRUÊNCIA POLINOMIAL
A congruência entre polinômios se dá da mesma forma dos números inteiros. Todos os polinômios que ao serem divididos por um polinômio D(x) gerarem um mesmo resto R(x) serão ditos congruentes e formarão um conjunto de polinômios.
Exemplos:
01. P(x) = x3 − x2 + 2x − 1 e G(x) = x4 + x2 + x são congruentes para o mesmo divisor D(x) = x2 + 1 pois ambos geram o mesmo resto R(x) = x quando divididos por D(x).
P(x) = x3 − x2 + 2x − 1 = Q1(x) ⋅ D(x) + R(x) = (x − 1)(x2 + 1) + x
G(x) = x4 + x2 + x = Q2(x) ⋅ D(x) + R(x) = (x2) · (x2 + 1) + x
Então escrevemos que P(x) ≡ G(x)
(mod(D(x))) ⇒ x3 − x2 + 2x − 1 ≡ x4 + x2 + x(mod(x2 + 1))
Vamos ver um exemplo de como utilizar a congruência em divisões de polinômios de graus elevados.
02. Sendo R(x) o resto da divisão de P(x) = 100x100 + 99x99 + 98x98 + 5x5 + 4x4 + 3x3 + 2x2 + x + 1 por D(x) = x2 − x + 1
O valor de R(–1) será:
Muitos tentam resolver este tipo de questão pelo método das chaves encontrando um padrão de decrescimento nos expoentes nas divisões sucessivas, mas esse padrão nem sempre aparece.
Um outro fato que é importante de ser observado é que o divisor geralmente não pode ser decomposto em outros fatores, mas geralmente é fator de um outro polinômio conhecido.
D(x) = x2 − x + 1 não pode ser decomposto em outros fatores de polinômios mas lembrando que x3 + 1=(x + 1) · (x2 − x + 1) sabemos que x3 + 1 é divisível por x2 − x + 1, assim x3 + 1 ≡ 0.
mod(x2 − x + 1) ⇒ x3 ≡− 1 mod(x2 − x + 1)
Então faremos aparecer x3 no polinômio
P(x) = 100x100 + 99x99 + 98x98 + 5x5 + 4x4 + 3x3 + 2x2 + x + 1
P(x) = 100(x3)33 ⋅ x + 99(x3)33 + 98(x3)32 ⋅ x2 + 4(x3) ⋅ x + 3x3 + 2x2 + x + 1 como x3 ≡ −1 mod(x2 − x + 1) então
100(−1)33 ⋅ x + 99(−1)33 + 98(−1)32 ⋅ x2 + 5(−1) ⋅ x2 + 4(−1) ⋅ x + 3(−1) + 2x2 + x + 1
−100x − 99 + 98x2 − 5x2 − 4x − 3 + 2x2 + x + 1 = 95x2 − 103x − 101
100x100 + 99x99 + 98x98 + 5x5 + 4x4 + 3x3 + 2x2 + x + 1 ≡ 95x2 − 103x − 101
mod(D(x))
Como o grau de R(x) ainda está igual ao grau de D(x) devemos dividir R(x) por D(x)
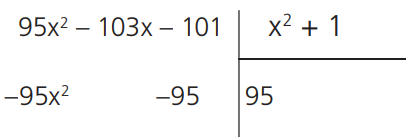
Logo
R(x) = -95x2 – 95 = – 95 (x2 + 1)
R(-1) = -95 ((-1)2 + 1) = -95 . 2 = – 190




