Um polinômio P(x) é divisível pelo ax + b se P(- b/a)=0
Exemplo:
Determinar o valor de p, para que o polinômio P(x) = 2×3 + 5×2 – px + 2 seja divisível por x – 2.
Resolução:
Se P(x) é divisível por x – 2, então P(2) = 0 . P(2) = 0 ⇒ 2 · 8 + 5 · 4 – 2p + 2 = 0 ⇒ 16 + 20 – 2p + 2 = 0 ⇒ p = 19
Resposta: p = 19.
DIVISÃO DE UM POLINÔMIO PELO PRODUTO (x – a)(x – b)
Vamos resolver o seguinte problema: calcular o resto da divisão do polinômio P(x) pelo produto (x – a)(x – b), sabendo-se que os restos da divisão de P(x) por (x – a) e por (x – b)são, respectivamente, r1 e r2.
Temos:
a é a raiz do divisor x – a, portanto P(a) = r1 (eq. 1)
b é a raiz do divisor x – b, portanto P(b) = r2 (eq. 2)
E para o divisor (x – a)(x – b) temos
P(x) = (x – a)(x – b) Q(x) + R(x) (eq. 3)
O resto da divisão de P(x) por (x – a)(x – b) é no máximo do 1º grau, pois o divisor é do 2º grau; logo R(x) = cx + d
Da eq.3 vem P(x) = (x – a)(x – b) Q(x) + cx + d
Fazendo
x = a ⇒ P(a) = c(a) + d (eq. 4)
x = b ⇒ P(b) = c(b) + d (eq. 5)
Das equações 1, 2, 4 e 5 temos:
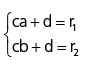
Resolvendo o sistema obtemos

Observações:
1ª) Se P(x) for divisível por (x – a) e por (x – b), temos:
P(a) = r1 = 0
P(b) = r2 = 0
Portanto, P(x) é divisível pelo produto (x – a)(x – b), pois:

2ª) Generalizando, temos:
Se P(x) é divisível por n fatores distintos (x – a1)(x – a2),…,(x – an) então P(x) é divisível pelo produto (x – a1)(x – a2), …,(x – an).
Exemplo:
Um polinômio P(x) dividido por x dá resto 6 e dividido por (x – 1) dá resto 8. Qual o resto da divisão de P(x) por x(x – 1)?
Resolução:
0 é a raiz do divisor x, portanto P(0) = 6 (eq. 1)
1 é a raiz do divisor x – 1, portanto P(1) = 8 (eq. 2)
E para o divisor x(x – 1) temos P(x) = x(x – 1) Q(x) + R(x) (eq. 3)
O resto da divisão de P(x) por x(x – 1) é no máximo do 1º grau, pois o divisor é do 2º grau; logo: R(x) = ax + b
Da eq.3 vem P(x) = x(x – 1) Q(x) + ax + b
Fazendo:
x = 0 ⇒ P(0) = a(0) + b ⇒ P(0) = b (eq. 4)
x = 1 ⇒ P(1) = a(1) + b ⇒ P(1) = a+b (eq. 5)
Das equações 1, 2, 4 e 5 temos:
{b = 6
{a + b = 8
Logo, b = 6 e a = 2.
Agora achamos o resto: R(x) = ax + b = 2x + 6
Resposta: R(x) = 2x + 6




