TEOREMA DAS BISSETRIZES
TEOREMA DA BISSETRIZ INTERNA
A bissetriz interna de um dos ângulos de um triângulo divide o lado oposto internamente em segmentos proporcionais aos lados adjacentes.
Seja AD a bissetriz interna do ângulo  de um triângulo ABC, então:

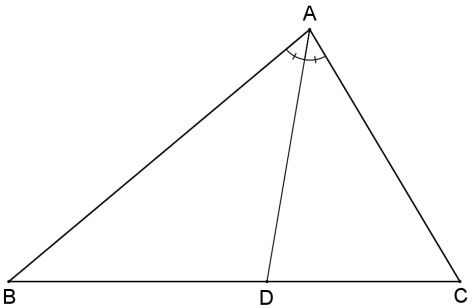
Exemplo: Em um triângulo ABC de lados AB = 12, AC = 8 e BC = 10, determine o maior segmento que a bissetriz interna do ângulo  determina sobre o lado BC.
Resolução:
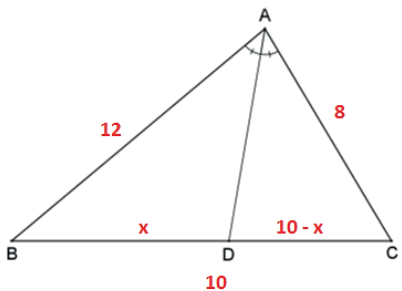
O maior segmento determinado pelo pé da bissetriz, D, sobre BC é o correspondente ao maior dos lados adjacentes ao vértice A, ou seja, BD.
Sendo BD = x, pelo teorema das bissetrizes internas, temos:

TEOREMA DA BISSETRIZ EXTERNA
A bissetriz externa de um dos ângulos de um triângulo divide o lado oposto externamente em segmentos proporcionais aos lados adjacentes.
Seja AE a bissetriz interna do ângulo  de um triângulo ABC, então:

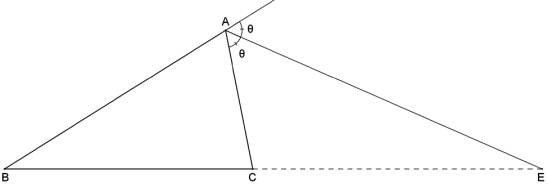
Exemplo: Em um triângulo ABC de lados AB=12, AC=8 e BC=10, determine a distância entre o pé da bissetriz externa do ângulo  e o vértice mais próximo do lado BC.
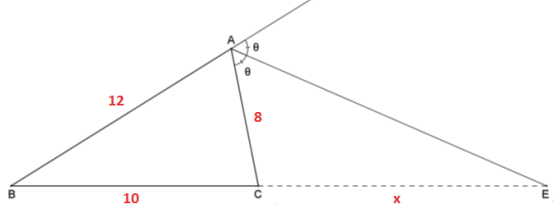
Resolução:
O pé da bissetriz externa está do junto ao menor lado. Assim, devemos calcular a medida de CE = x.
Pelo teorema das bissetrizes externas, temos:





