Sólidos homogêneos
Veja abaixo.
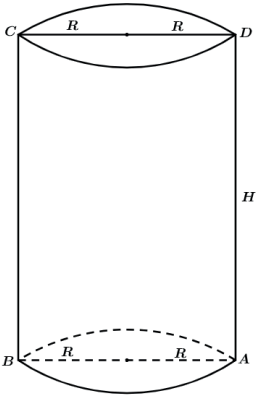
Temos um cilindro circular reto e vamos fazer um corte utilizando um plano paralelo as bases exatamente na metade da sua altura.
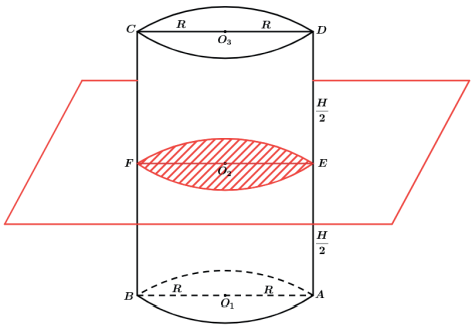
Com isso geramos 2 novos cilindros retos, mas com alturas H/2 porém, pelo fato de ser um sólido homogêneo, qualquer corte por um plano paralelo as bases irão gerar o mesmo polígono das bases e de mesma área S.
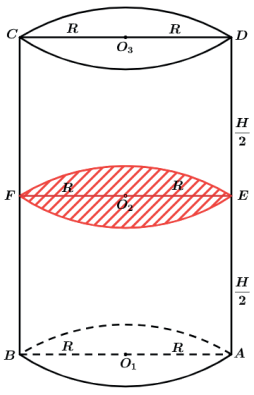
Todos os círculos, de centros O1, O2 e O3 possuem as mesmas áreas πR2, fazendo com que seus volumes dependam somente das suas alturas. Assim a fração da altura que se efetua o corte define a fração do volume. Assim no nosso exemplo, cada sólido resultante do corte terá metade do volume do sólido inicial.
Não é à toa que se uma receita pede que seja utilizado metade do volume de uma lata de leite condensado nós utilizamos o leite condensado até a metade da lata. Se enchermos um cubo até um terço de sua altura teremos um terço do volume total e assim para qualquer sólido homogêneo.
Observação:
Nos sólidos homogêneos os cortes em diagonal também geram metade do volume.
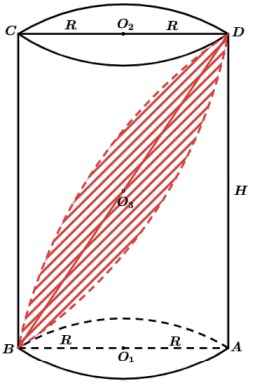
Cada sólido resultante tem metade do volume do sólido original.
PIRÂMIDES E CONES
O estudo para as pirâmides retas e cones retos se dá da mesma maneira quando seccionados por planos paralelos a suas bases.
Utilizando a mesma ideia dos sólidos homogêneos fica fácil perceber que após um corte por um plano paralelo a base os sólidos resultantes não terão seus volumes ligados diretamente a proporção de suas alturas. Dessa forma temos de recorrer a semelhança entre os sólidos. Tomemos o cone reto abaixo.
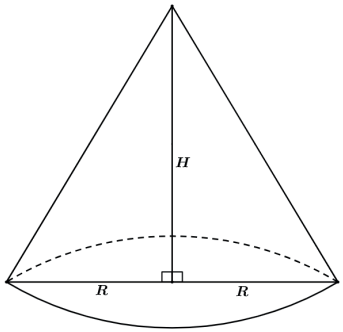
Vamos fazer uma secção por um plano paralelo a base de centro O do cone.
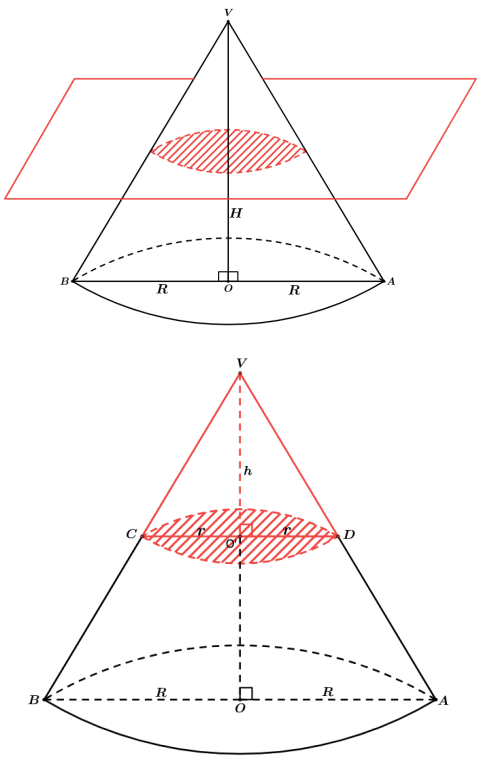
Vemos que o novo cone gerado, VCD de centro O’, também tem como base um círculo, porém de raio diferente do cone VAB de centro O. Dessa forma seu volume não fica dependendo somente de sua altura h como também passa a depender desse seu novo raio da base r, que é definido através de uma semelhança.
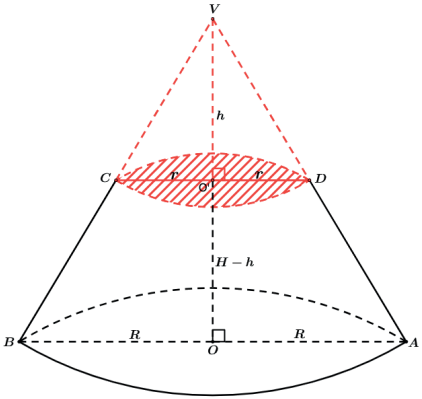
Tronco é o sólido resultante da retirada do sólido superior ao plano de corte (sólido que é semelhante ao sólido original). Vale lembrar que os troncos eles não são sólidos semelhantes com os sólidos originais ou os retirados, utilizá-los na semelhança é um erro muito comum.
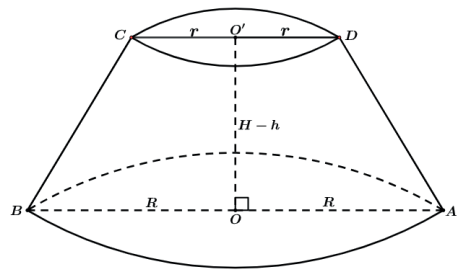
A figura acima ilustra um tronco de cone reto, resultado da remoção do cone menor do cone maior.
Chegaremos ao seu volume utilizando semelhança entre os sólidos encontrando os volumes do sólido maior e do menor e no final fazendo a diferença entre seus volumes.
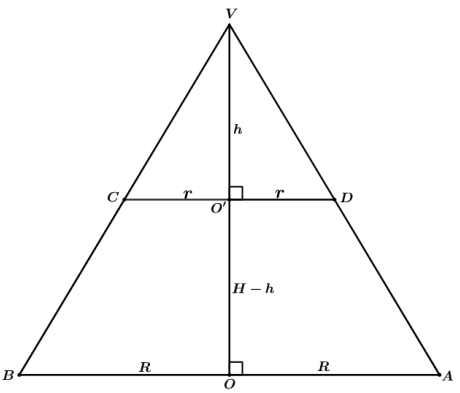
Vamos “ver” de frente os sólidos e ver os triângulos que temos. Quando fazemos a semelhança de medidas lineares, medidas de comprimento, apenas uma dimensão, dizemos que essa razão de semelhança é k. Assim para os triângulos da figura teríamos:

Sabemos que quando fazemos razões entre áreas de figuras planas nossa razão passa a ser k2. Agora quando fizermos razões entre volumes teremos a razão k3.
Dessa forma podemos fazer razões entre os volumes dos sólidos VCD e VAB.

Assim para encontrarmos k basta utilizarmos a razão que nos for mais conveniente, seja r/R ou h/H ou qualquer outra razão linear.
Depois de encontrado o volume do sólido “menor” para encontrarmos o volume do tronco basta efetuar a subtração entre os volumes dos cones “maior” e “menor”.
Exemplo:
Um cone reto de volume igual a 64 cm3 é seccionado na metade de sua altura por um plano paralelo a sua base. Calcular o volume do tronco resultante.
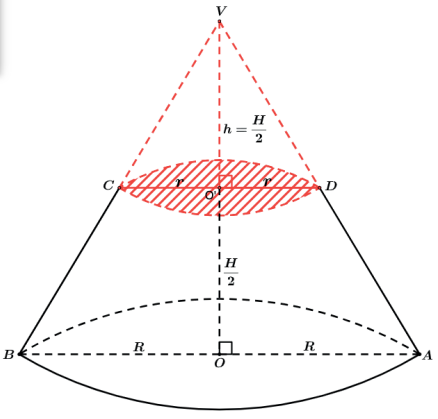
Ao utilizarmos a subtração teremos
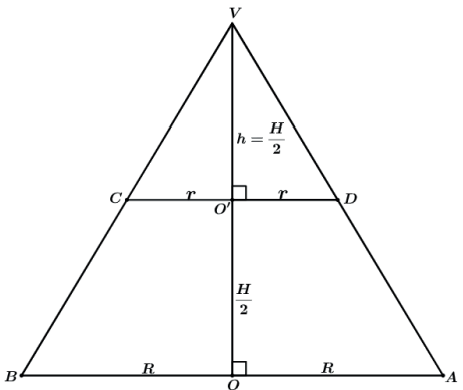

Assim fazendo a semelhança entre os volumes dos 2 cones
Assim o volume do cone “menor” é 8 cm3 e consequentemente o volume do tronco gerado será Vtronco = 64 − 8 = 56 cm3.
Existem 2 fórmulas que calculam direto os volumes do tronco de cone e de pirâmide quando são conhecidas as medidas das 2 bases e da altura do tronco.
I. Tronco de cone
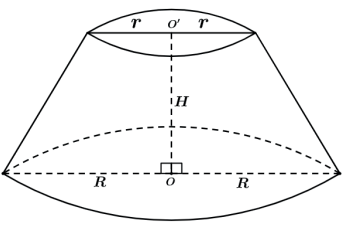

R → Raio da base maior
r → Raio da base menor
H → Altura do tronco
II. Tronco de pirâmide
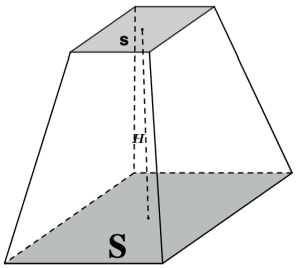
* A fórmula serve para troncos de pirâmides retas de qualquer base, a figura utilizou a quadrangular só para exemplificar.

S → Área da base maior
s → Área da base menor
H → Altura do tronco
TRONCO DE CONE RETO DE REVOLUÇÃO
O tronco de cone reto é obtido pela rotação de um trapézio retângulo em torno da reta suporte do lado reto (altura do trapézio).
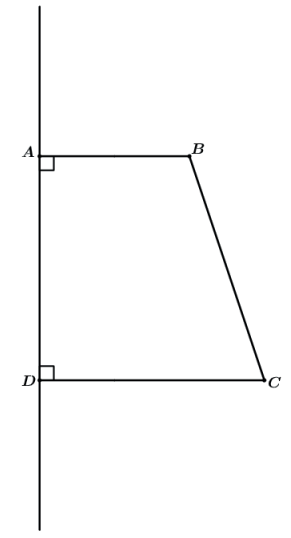
Assim teremos o tronco de cone reto com o raio da base maior sendo CD, da base menor sendo AB e altura AD.
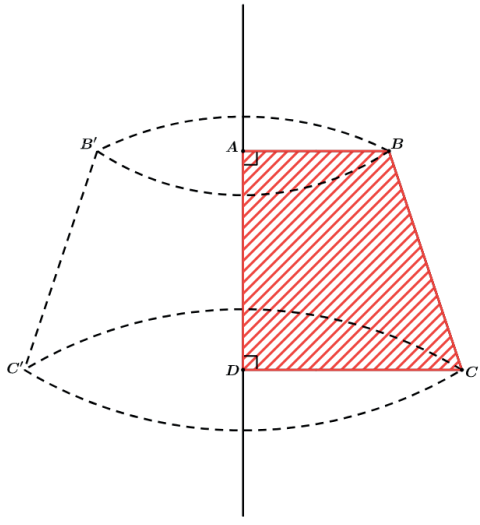
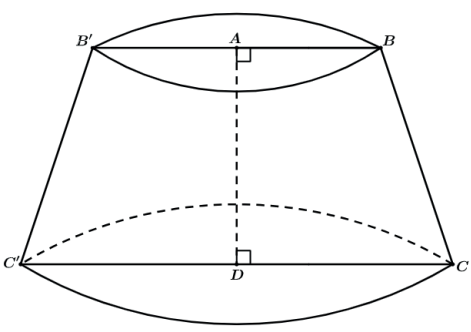
Para calcular o volume do tronco de cone podemos utilizar a conhecida fórmula

Vamos ver exemplos de troncos de revolução vazados.
I. Sólido de revolução gerado pela rotação de um triângulo retângulo ABC, retângulo em A, em torno de uma reta r, paralela a AB e distando d de AB.
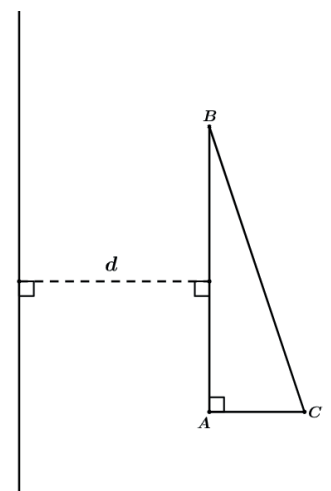
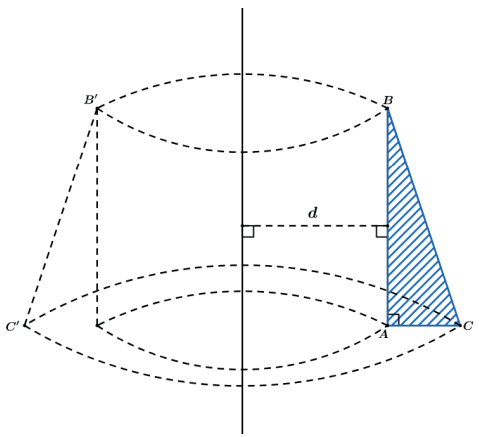
Teremos o tronco de cone BCC’B’ vazado pelo cilindro ABB’A’.
II. Sólido de revolução gerado pela rotação de um trapézio retângulo ABCD, em torno de uma reta r, paralela a AB e distando d de AB.
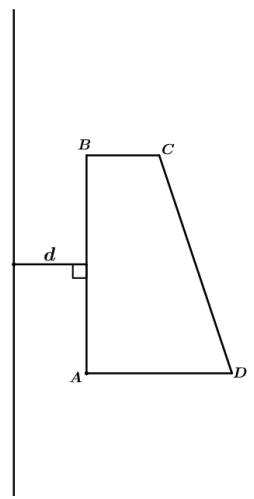
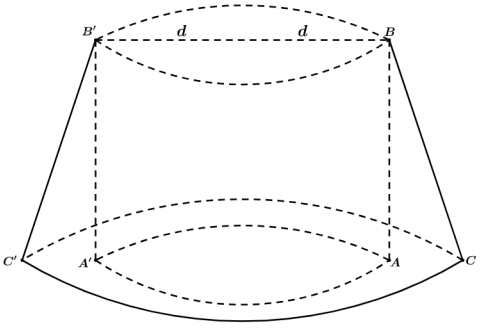
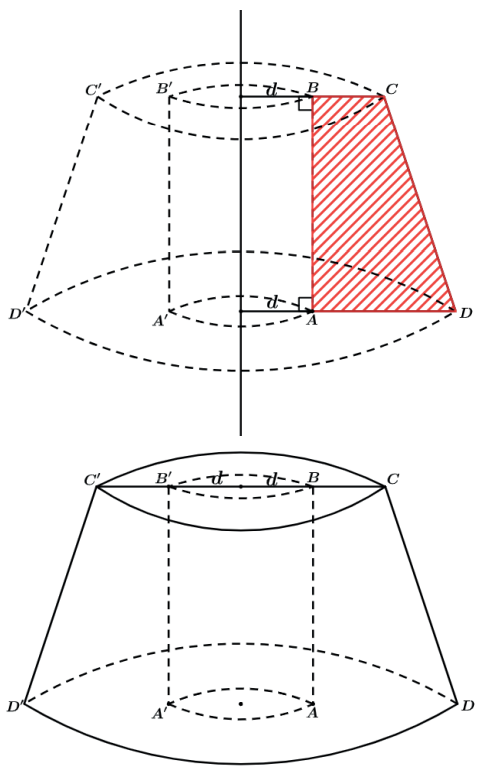
Teremos o tronco de cone CDD’C’ vazado pelo cilindro ABB’A’.




