Sistemas Lineares: Equação

EQUAÇÃO LINEAR

É Toda equação da forma a₁x₁ + a₂x₂ +⋯+ a_nx_n = b onde a₁, a₂, ⋯, a_n são números reais que recebem o nome de coeficientes das incógnitas x₁, x₂,⋯ x_n e b é um número real chamado termo independente.

Observação: Quando b = 0, a equação recebe o nome de linear homogênea.

Exemplos:

SISTEMA LINEAR

Definição: Um conjunto de equações lineares da forma 

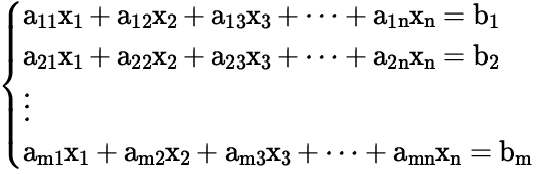
é um sistema linear de m equações e n incógnitas.

SOLUÇÃO DO SISTEMA LINEAR

Chamamos de solução do sistema a n-upla de números reais ordenados (r₁, r₂,⋯,r_n) que é, simplesmente, solução de todas equações do sistema.

MATRIZES ASSOCIADAS A UM SISTEMA LINEAR 

MATRIZ INCOMPLETA

É a matriz A, formada pelos coeficientes das incógnitas do sistema.

Exemplos:

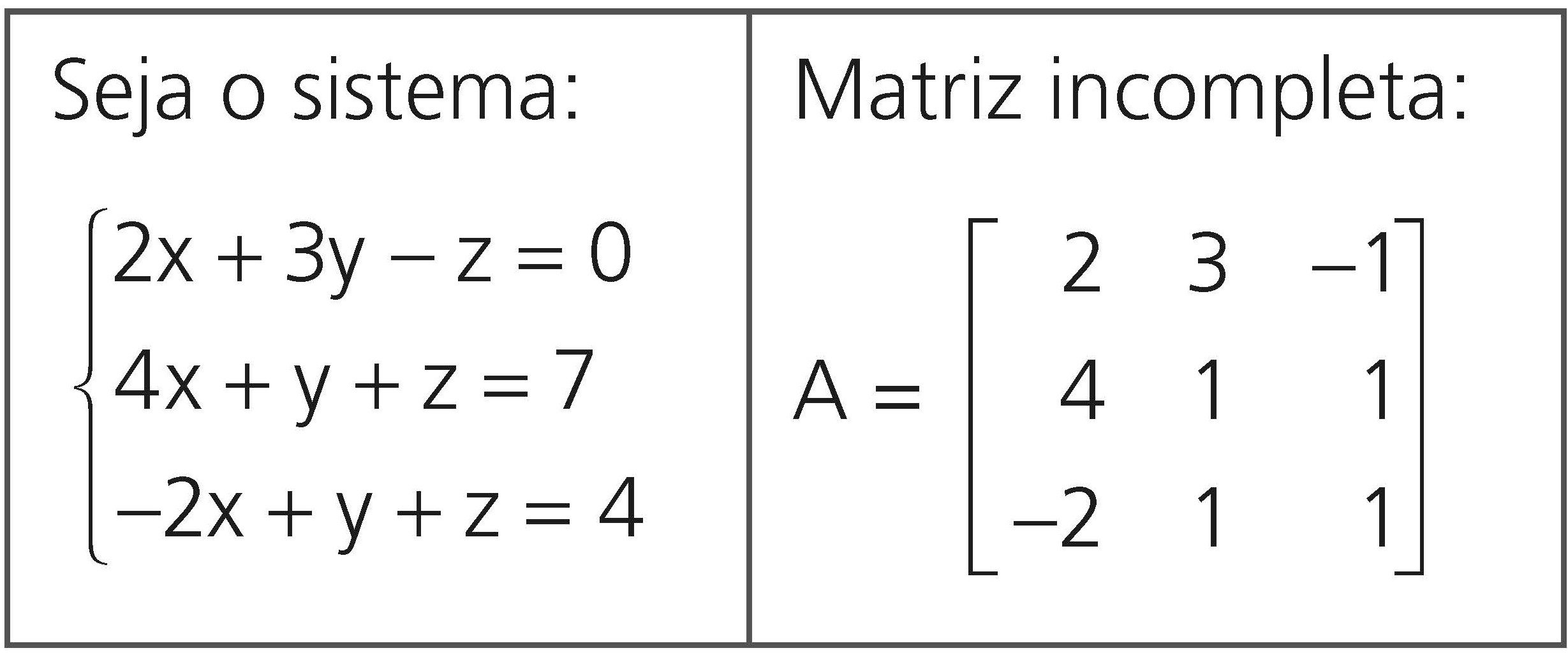
MATRIZ COMPLETA

É a matriz B, que obtemos ao acrescentarmos à matriz incompleta uma última coluna formada pelos termos independentes das equações do sistema. Assim a matriz completa referente ao sistema anterior é

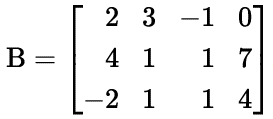
SOLUÇÕES DE UM SISTEMA HOMOGÊNEO

A n-upla (0, 0, 0, …, 0) é sempre solução de um sistema linear homogêneo com incógnitas e recebe o nome de solução trivial. Quando existem, as demais soluções são chamadas não-triviais.