Retas

EQUAÇÃO REDUZIDA DA RETA

RETA VERTICAL

A equação de uma reta paralela ao eixo Oy é x = k, onde k é constante. Neste caso, não existem os coeficientes angular e linear.

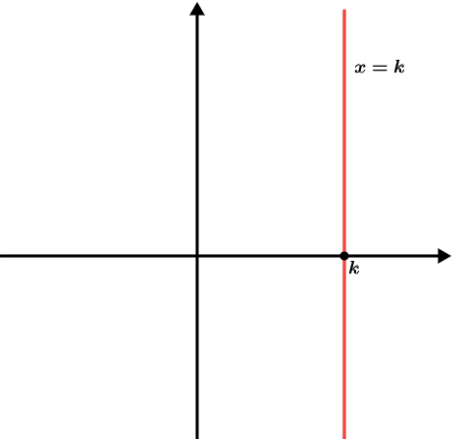
Sabemos que para determinar uma reta é necessário, no mínimo, que tenhamos 2 pontos distintos ou também podemos determinar uma reta conhecendo um ponto e o ângulo formado pela reta e o eixo Ox^↔.

É conhecido, desde o estudo da função afim, que uma reta é definida pela equação y = ax + b. Se conhecermos 2 pontos distintos A(x_A ,y_A) , B(x_B, y_B) podemos fazer

Se utilizarmos as nomenclaturas utilizadas em geometria analítica a nossa equação será y = mx + n, sendo chamada de equação reduzida. Nessa equação teremos 2 elementos muito importantes.

m → Coeficiente angular

O coeficiente angular (m) será o responsável pelo ângulo formado pela reta e o eixo Ox^↔. Como vimos o coeficiente angular será m = ^Δx/_Δy , que ao olharmos para a figura abaixo veremos que ^Δx/_Δyé a tangente do ângulo α.

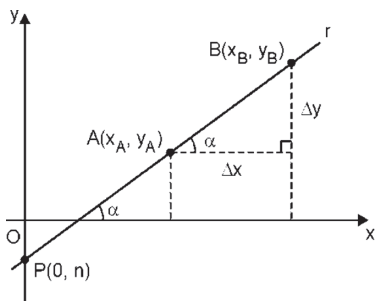
Logo m = tg α = ^Δx/_Δy

n →Coeficiente linear

O coeficiente linear (n) será o responsável por determinar a intersecção da reta com e eixo Oy^↔. Toda intersecção com o eixo Oy^↔ se dá num ponto da forma (0, y).

Assim y = m ⋅ 0 + n ⇒ y = n, então o ponto de intersecção será (0, y).

Vamos ver um exemplo

Exemplo:

Encontrar equação de reta que passa pelos pontos A(2, 1) e B(-3, 4)

Podemos usar o seguinte: (y – y₀) = m(x – x₀) onde x₀ e y₀ são as coordenadas de um ponto que pertença a reta.

Ou podemos também simplesmente substituir as coordenadas do ponto A ou do ponto B na equação y =− ³/₅ x + n.

Substituindo as coordenadas do ponto A na nossa reta

ProBizu: Tenha bastante atenção com pegadinhas que são colocadas. A reta só está na sua forma reduzida quando y está realmente isolado. Por exemplo 2y = x + 2 não tem seu m =1 e n =2 pois o y não está isolado na equação. Temos de fazer y = ^x+2/₂ = ^x/₂ +1 para só assim determinarmos m = ¹/₂ e n = 2. Atenção!

EQUAÇÃO DE RETA POR DETERMINANTE

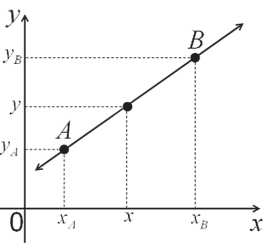
Introduzindo o ponto (x, y) na reta formada pelos pontos A e B teremos 3 pontos alinhados, onde vimos que a condição para estarem alinhados é

Exemplo: A equação de reta que passa pelos pontos A(2, 1) e B(–3, 4) é

INTERSECÇÃO DE DUAS RETAS

A teoria da intersecção entre duas retas é a mesma para quaisquer duas curvas, que é a resolução de um sistema entre as equações que representam cada uma das curvas.

A forma de resolução do sistema é a mesma da álgebra, podendo se dar pelo método da adição ou da substituição.

Exemplo: O ponto de intersecção entre as retas de equações y = x − 3 e 2y − 3x = 4 é

ÂNGULO ENTRE DUAS RETAS

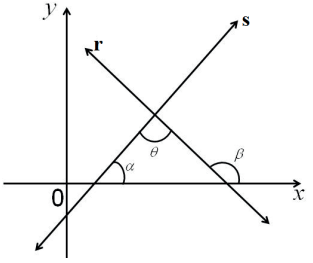
θ = β − α

Aplicando a função tangente em ambos os lados da igualdade teremos tg θ = tg (β − α) e como m_r = tg β e m_s = tg α teremos pela fórmula de subtração de tangente:

Exemplo:

Determine o ângulo formado entre as retas r: y = 3x + 4 e s: y =−2x + 8

Resolução:

Vamos determinar o coeficiente angular de cada uma das retas dadas.

Para a reta r, temos:

y = 3x + 4
m_r = 3

Para a reta s, temos:

y = −2x + 8
m₅ = −2

Aplicando a fórmula do ângulo entre duas retas, obtemos:

Portanto, α = arctg 1 ou α = 45^∘

PARALELISMO E PERPENDICULARISMO

A equação reduzida da reta é y = mx + n, onde m é o coeficiente angular e n é coeficiente linear. Onde m = tg α e α é o ângulo formado entre a reta e o eixo Ox^↔.

n é o ponto de intersecção da reta com o eixo Oy^↔.

RETAS PARALELAS

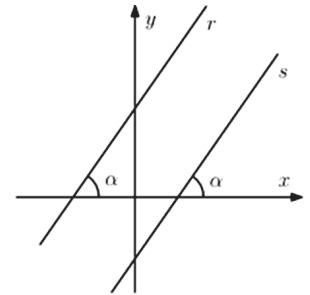
Como as retas r e s possuem o mesmo ângulo α com o eixo Ox^↔ então m_r = m_s.

RETAS PERPENDICULARES

Na equação ^mr−ms/_1+mr⋅ms , do ângulo entre 2 retas para termos θ = 90º temos que ^mr−ms/_1+mr⋅ms não pode existir, daí 1 + m_r⋅ m_s = 0 ⇒ m_r ⋅ m_s= −1.

Exemplo: As equações de retas r : y = −2x + 3, s : y = ^x/₂ − 4 e t : y = −2x + 3.

As restas r e t possuem o mesmo coeficiente angular, m_r = m_t. Daí r e t são paralelas.

As retas r e s ou s e t possuem os coeficientes angulares inversos simétricos entre si, m_r ⋅ m_s = -2 (¹/₂) = -1. Daí r// t que são perpendiculares a s.

OUTRAS EQUAÇÕES DE RETA

EQUAÇÃO COMPLETA DA RETA

Da equação reduzida y = mx + n quando isolamos todos os termos de um mesmo lado da igualdade passamos a ter os termos ax + by + c = 0 com a, b e c ∈ ℤ, que é a equação completa da reta.

Exemplo:

EQUAÇÃO SEGMENTÁRIA DA RETA

Da equação completa da reta ax + by + c = 0 isolaremos o termo c de um lado da igualdade, ax + by = –c e dividiremos todos os termos por -c, assim − ^a/_c x −^b/_c y = 1.

Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:

As equações paramétricas são duas equações que representam a mesma reta utilizando uma incógnita t. Essa incógnita recebe o nome de parâmetro e faz a ligação entre as duas equações que representam a mesma reta.

Vamos a um exemplo prático.

Seja a equação x − 2y + 3 = 0 → 2y = x + 3 → y = ^x+3/₂. Vamos escolher uma parametrização arbitrária para y, por exemplo y = 2t + 1.

Para voltarmos para equação completa ou reduzida basta isolarmos t em ambas equações e igualá-los.

DISTÂNCIA DE PONTO A RETA

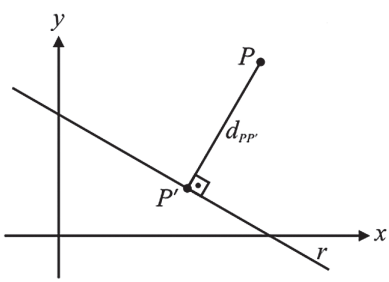
Sendo a equação da reta r: ax + by + c = 0 e P(x₀, y₀) temos

Exemplo:

01. A distância do ponto P(–1, 1) a reta de equação y =−2x + 3 é

02. Dado o ponto A(3, –6) e r : 4x + 6y + 2 = 0. Estabeleça a distância entre A e r

DISTÂNCIA ENTRE DUAS RETAS PARALELAS

Se r//s de equações r: ax + by + c1 = 0 e s : ax + by + c₂ = 0

Nota: duas retas paralelas, quando na forma completa, possuem mesmos coeficientes a e b.

Exemplo:

Calcula a distância entre as retas r: 2x + 3y = 4 e s: 2x + 3y = 1.

PONTO SIMÉTRICO

A simetria ou reflexão em relação a um objeto, que na maior parte das vezes é uma reta, deve ser tratada como a reflexão em relação a um espelho.

Vamos primeiramente verificar a reflexão em relação aos eixos coordenados.

REFLEXÃO EM RELAÇÃO EIXO DAS ABSCISSAS (Ox^↔)

Quando fazemos a reflexão ou simetria em relação ao eixo das abscissas verificamos que a abscissa do ponto em questão se mantém enquanto a ordenada do ponto em questão é simétrica. Dessa forma sendo P’ o ponto simétrico de P em relação ao eixo Ox^↔ temos que

P(x, y) ⇒ P'(x, −y)

Exemplo:

O simétrico do ponto A(–2, –4) em relação eixo das abscissas é o ponto A'(–2, 4).

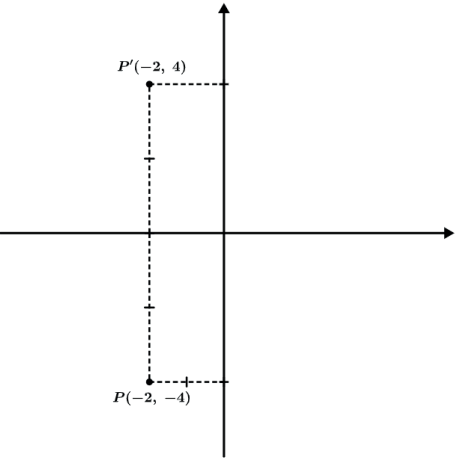
REFLEXÃO EM RELAÇÃO EIXO DAS ABSCISSAS (Oy^↔)

Quando fazemos a reflexão ou simetria em relação ao eixo das ordenadas verificamos que a ordenada do ponto em questão se mantém enquanto a abscissa do ponto em questão é simétrica. Dessa forma sendo P’ o ponto simétrico de P em relação ao eixo Ox↔ temos que

P(x, y) ⇒ P'(−x, y)

Exemplo:

O simétrico do ponto A(1, 3) em relação eixo das abscissas é o ponto A'(–1, 3).

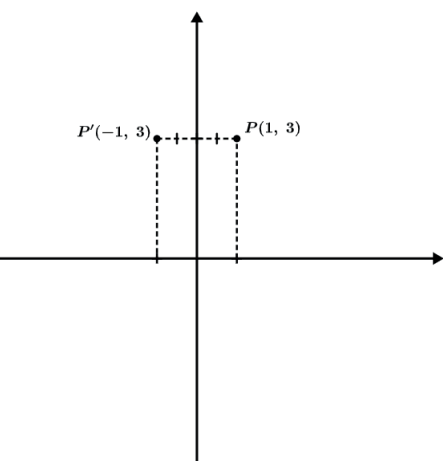
REFLEXÃO EM RELAÇÃO A UMA RETA DADA

Seja um ponto P(x, y) e uma reta r : ax + by + c = 0.

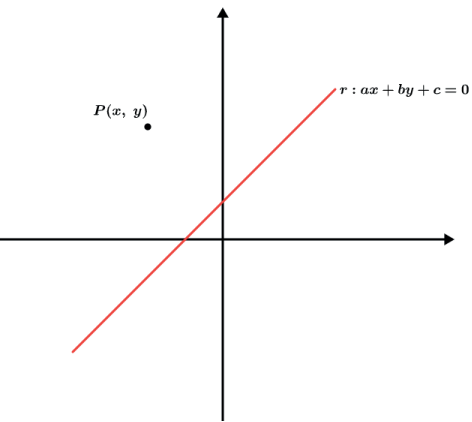
Definiremos o ponto P'(m, n) como o ponto simétrico do ponto P em relação a reta r.

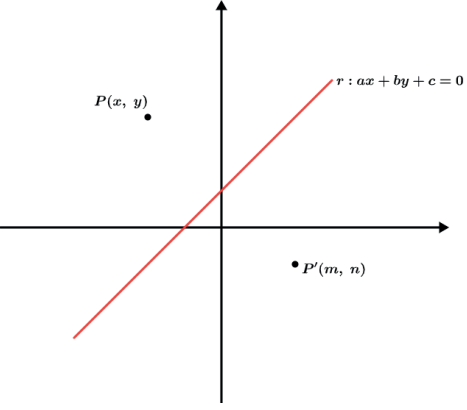
O ponto P’ define com o ponto P uma reta perpendicular a reta r e ainda P e P’ estão a mesma distância da reta r.

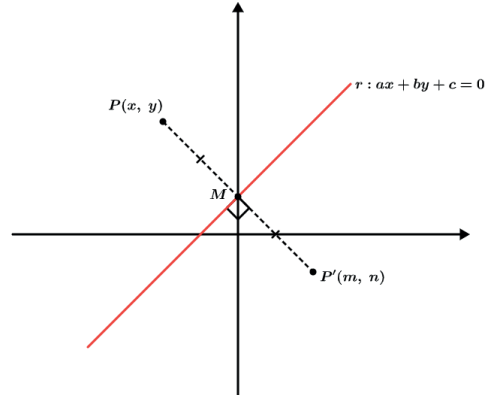
Sabendo disso, para determinarmos um ponto simétrico de um ponto dado em relação a uma reta, devemos seguir os seguintes passos.

1. Encontrar a equação da reta perpendicular a reta dada. Faremos isso a partir da relação existente entre os coeficientes angulares de duas retas perpendiculares entre si (m₁ ⋅ m₂= −1).
2. Iremos encontrar o ponto de interseção entre a reta perpendicular que encontramos com reta dada. Faremos isso colocando as duas equações de reta em sistema linear de duas equações e duas incógnitas.
3. A interseção encontrada é o ponto médio do segmento determinado pelo ponto dado e seu ponto simétrico. Por fim iremos utilizar o ponto de interseção como o ponto médio para determinar o ponto simétrico P’.

Vamos ver o exemplo a seguir.

Exemplo:

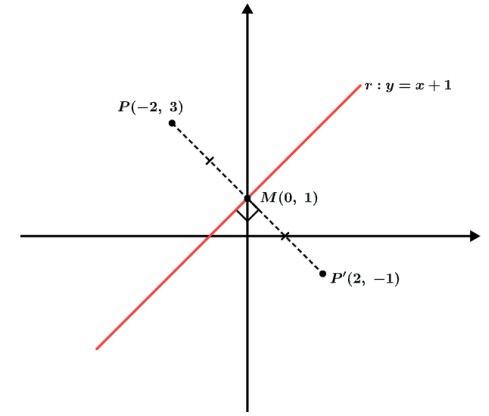
Encontre o ponto simétrico do ponto P(–2, 3) em relação a reta r: y = x + 1.

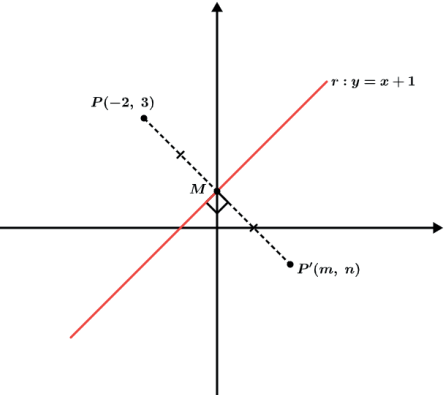
Vamos chamar o ponto simétrico do ponto P de P'(m, n) e vamos determinar a equação da reta PP’^↔, que iremos chamar de reta s, a partir do coeficiente angular da reta r.

Coeficiente angular da reta r: y = x + 1

m_r = 1

Coeficiente angular da reta s, perpendicular a r.

m_r ⋅ m_s = −1 ⇒ m_s = −1

Equação da reta s

y = m_s ⋅ x + n ⇒ y = −x + n

Como a reta s passa pelo ponto P(–2, 3) temos que P ∈ s e assim

3 = −(−2) + n ⇒ n = 3 − 2 = 1

E assim nossa reta s é y = –x + 1

Agora iremos encontrar a interseção entre as retas r e s resolvendo o sistema de equações:

Logo nosso ponto de interseção será o ponto M(0, 1).

O ponto M(0, 1) será o ponto médio dos pontos P(–2, 3) e P'(m, n) e assim

Assim o ponto P’, simétrico do ponto P(–2, 3) em relação a reta r : y = x + 1, é o ponto P'(2, -1).

Exemplo:

Considere as retas r e s definidas por r: kx − (k + 2)y = 2 e s : ky − x = 3k. Determine k de modo que:

a) r e s sejam concorrentes
b) r e s sejam paralelas
c) r e s sejam coincidentes.

Resolução:

Pela definição, retas concorrentes possuem um ponto de interseção, as paralelas nenhum ponto de interseção e as coincidentes, todos seus pontos são de interseção. Nos termos de Geometria Analítica, analisamos os coeficientes angulares das retas: