DEFINIÇÃO DE ÁREA
Cada figura plana está associada a um número positivo chamado área que possui as seguintes propriedades:
P1 : Figuras planas congruentes possuem a mesma área, ou seja, são equivalentes.
P2 : Se uma figura plana P for decomposta em duas outras P1 e P2 então a área de P é a soma das áreas de P1 e de P2.
P3 : A área de um retângulo de base b e altura h é igual ao produto b ⋅ h.
RETÂNGULO
Como estabelecido na propriedade P1, a área de um retângulo de base b e altura h é igual ao produto b⋅h.
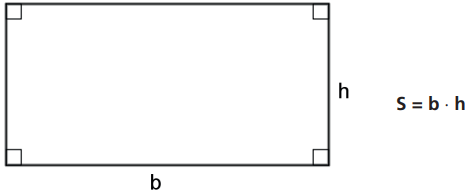
Exemplo: Calcule a área do retângulo da figura.

PARALELOGRAMO
A área de um paralelogramo de base b e altura h é igual ao produto b ⋅ h, ou seja, é igual à área do retângulo de mesma base e altura.
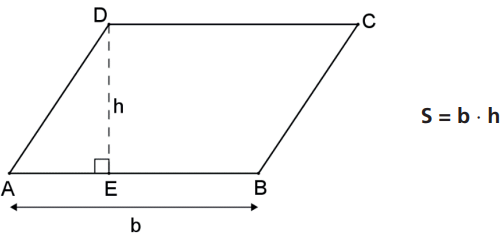
Demonstração:
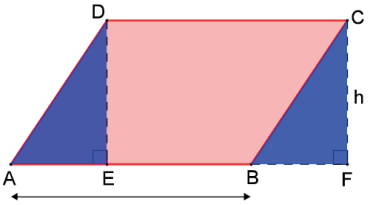
SADE = SBCF ⇒ SABCD = SDEFC = b ⋅ h
Exemplo:
Calcule a área do paralelogramo da figura.
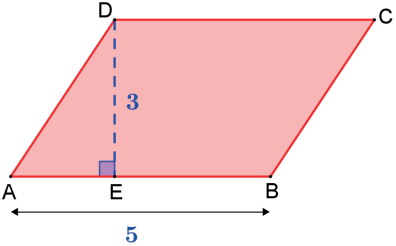
SABCD =5 ⋅ 3 = 15 u . a.
TRIÂNGULOS
Nessa seção serão apresentadas diversas fórmulas para o cálculo da área de um triângulo.
A área de um triângulo é igual à metade do produto de um dos lados pela altura relativa a ele.
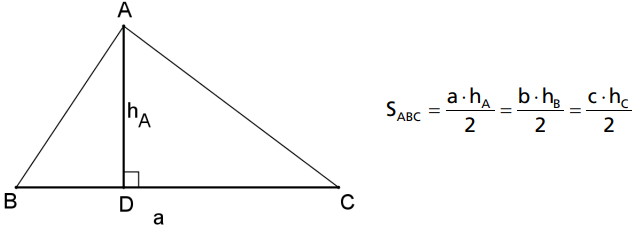
Demonstração:
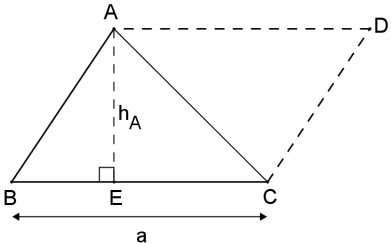
Sejam AD || BC e CD || AB, então o #ABCD é um paralelogramo e △ABC ≡ △CDA(L.L.L.).

Note que, quando o triângulo é obtusângulo, o pé da altura pode estar no prolongamento do lado, mas a fórmula funciona do mesmo modo.
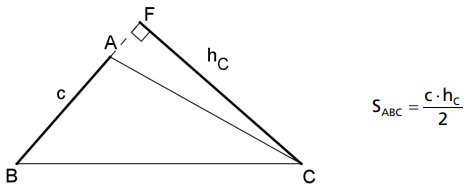
Exemplo: Calcule a área dos triângulos das figuras a seguir.
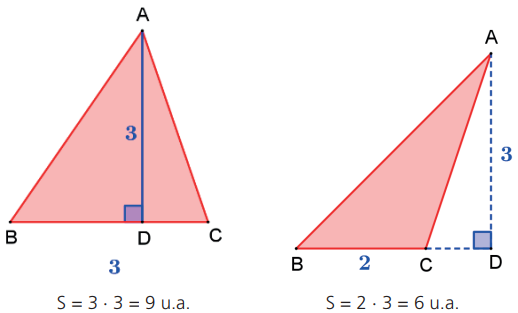
A área de um triângulo é igual à metade do produto de dois lados adjacentes multiplicado pelo seno do ângulo entre eles.
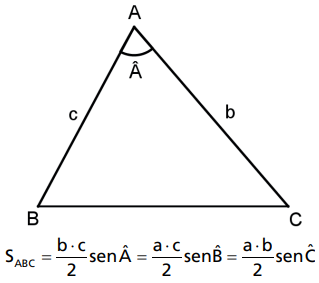
Demonstração:
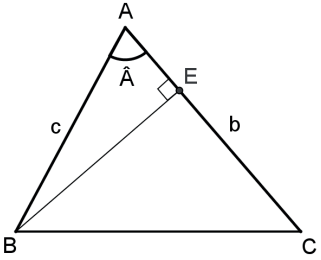
Seja BE a altura relativa ao lado AC do ΔABC, então SABC = AC⋅BE/2.

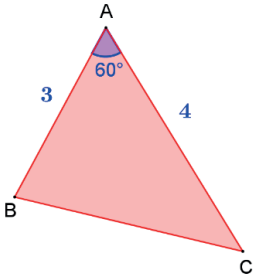
Exemplo:
Calcule a área do triângulo da figura a seguir.

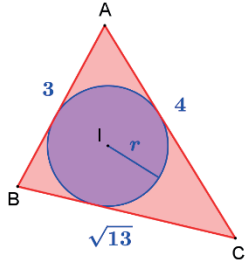
A área de um triângulo é igual ao produto de seu semiperímetro pelo raio do círculo inscrito nesse triângulo.
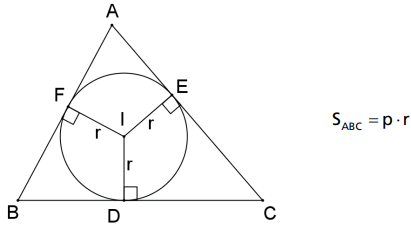
Demonstração:

Exemplo:
Calcule a área do triângulo da figura a seguir:


A área de um triângulo é igual ao produto da diferença entre o semiperímetro e um dos seus lados pelo raio do círculo ex-inscrito relativo a esse lado.
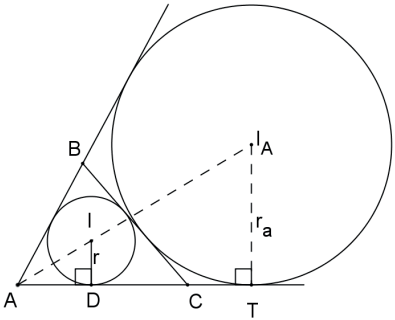
SABC = (p − a) ⋅ ra = (p − b) ⋅ rb = (p − c) ⋅ rc
Demonstração:
Na figura AD = p − a e AT = p.

A área de um triângulo é igual ao produto dos três lados dividido pelo quádruplo do raio do círculo circunscrito a esse triângulo.
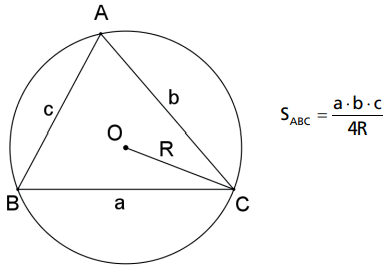
Demonstração:
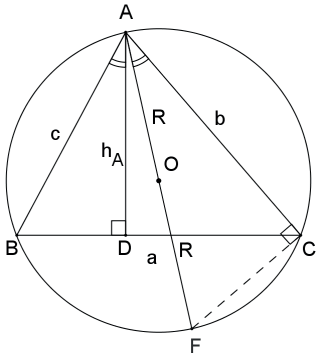
AOF é um diâmetro do círculo circunscrito, então AC^F = 90∘.

Exemplo:
Calcule a área do triângulo da figura a seguir, sabendo que:

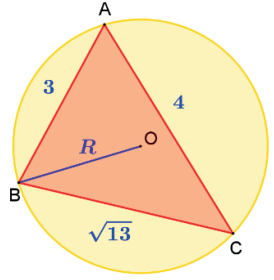

A área de um triângulo é igual ao dobro do quadrado do raio do círculo circunscrito multiplicado pelo produto dos senos de seus ângulos.
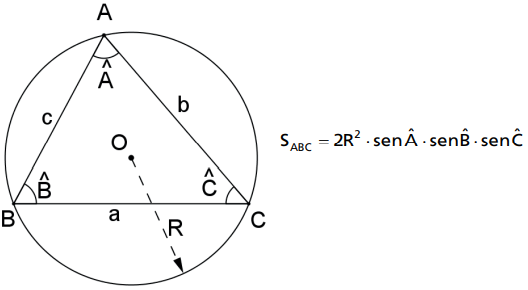
Demonstração:
Aplicando a lei dos senos ao ΔABC:

FÓRMULA DE HERON
A área de um triângulo é igual à raiz quadrada do produto do semiperímetro pela diferença entre o semiperímetro e cada um dos lados do triângulo.
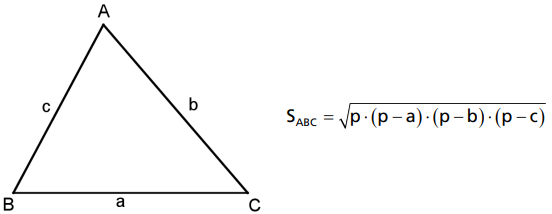

Demonstração:
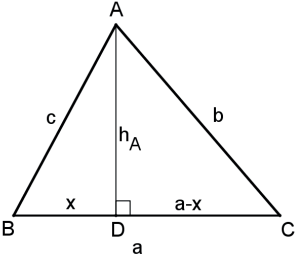
Aplicando o teorema de Pitágoras nos ΔABC e ΔACD, temos:

Exemplo:
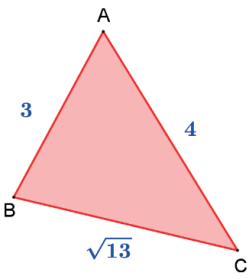
Calcule a área do triângulo da figura.

A área de um triângulo é igual à raiz quadrada do produto do raio do círculo inscrito e dos três raios dos círculos ex-inscritos ao triângulo.
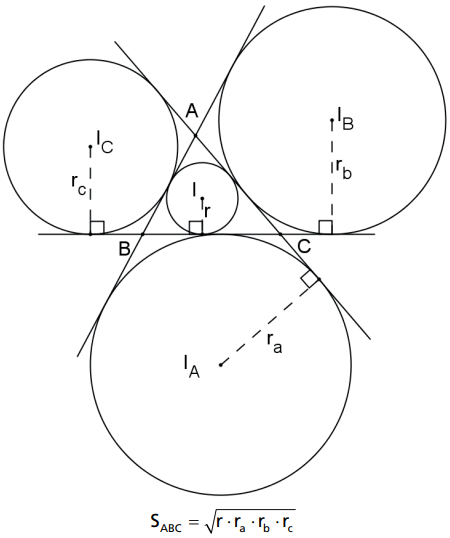
Demonstração:

A área de um triângulo é igual à raiz quadrada da metade do produto do raio do círculo circunscrito por cada uma das três alturas do triângulo.
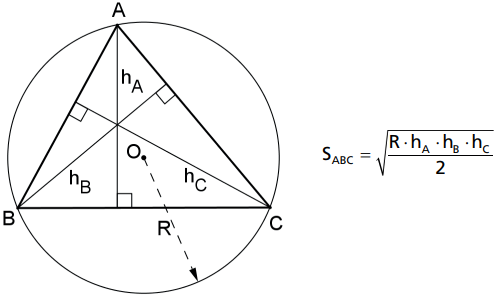
Demonstração:

TEOREMA DE BURLET
Em um triângulo retângulo, a área é igual ao produto dos segmentos determinados pelo círculo inscrito sobre a hipotenusa.
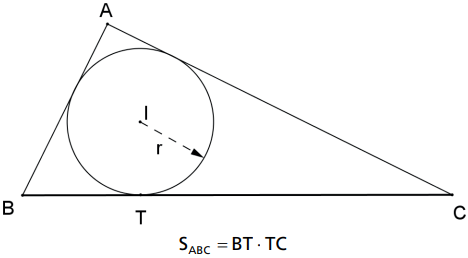
Demonstração:





