Geometria Analítica Plana: Reta – Paralelismo e perpendicularismo

O conceito de paralelismo e perpendicularismo entre retas é fundamental na geometria. Quando duas retas são paralelas, elas nunca se encontram, mantendo uma distância constante. Já retas perpendiculares se cruzam formando ângulos retos.

PARALELISMO E PERPENDICULARISMO

A equação reduzida da reta é y = mx + n, onde m é o coeficiente angular e n é coeficiente linear. Onde m=tg α e α é o ângulo formado entre a reta e o eixo Ox↔.

n é o ponto de intersecção da reta com o eixo Oy↔.

RETAS PARALELAS

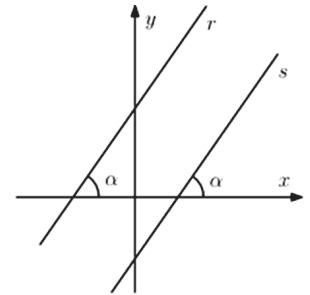
Como as retas r e s possuem o mesmo ângulo α com o eixo Ox↔ então mr = ms.

RETAS PERPENDICULARES

Na equação ^mr−ms/_1+mr⋅ms , do ângulo entre 2 retas para termos θ = 90º temos que^mr−ms/_1+mr⋅msnão pode existir, daí 1+mr⋅ms = 0 ⇒ mr⋅ms = −1.

Exemplo: As equações de retas r : y = −2x + 3, s : y = ^x/₂ − 4 e t : y=−2x + 3.

As restas r e t possuem o mesmo coeficiente angular, m_r = m_t. Daí r e t são paralelas.

As retas r e s ou s e t possuem os coeficientes angulares inversos simétricos entre si, mr ⋅ ms = -2 (¹/₂) = -1. Daí r// t que são perpendiculares a s.