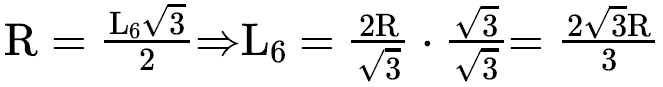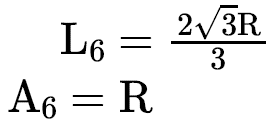RELAÇÕES MÉTRICAS NOS POLÍGONOS REGULARES
TRIÂNGULO EQUILÁTERO INSCRITO
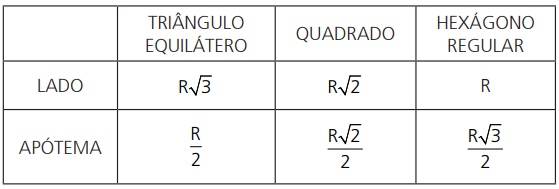
O lado de um triângulo equilátero (regular) inscrito em uma circunferência de raio R é I3 = R√3 e o seu apótema é a3 = R/2.
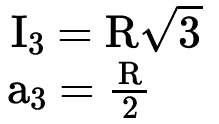
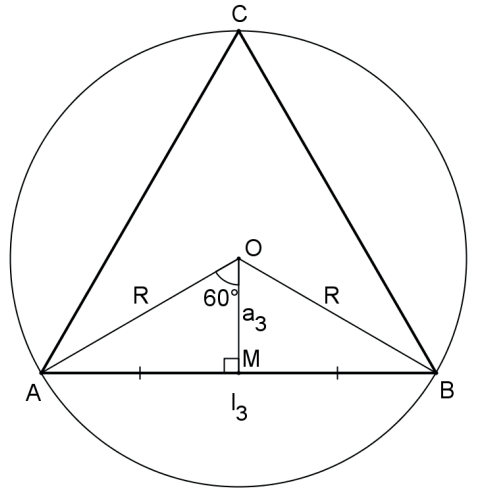
Demonstração:
No triângulo retângulo AOM da figura temos:
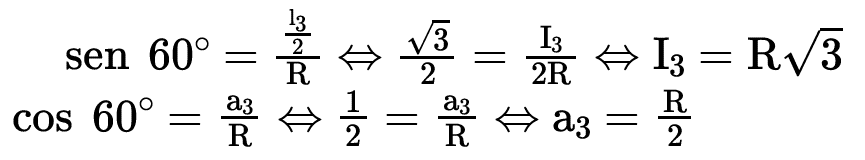
QUADRADO INSCRITO
O lado de um quadrado (quadrilátero regular convexo) inscrito em uma circunferência de raio R é I4 = R√2 e o seu apótema é a4 = R√2/2.
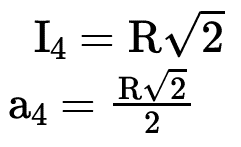
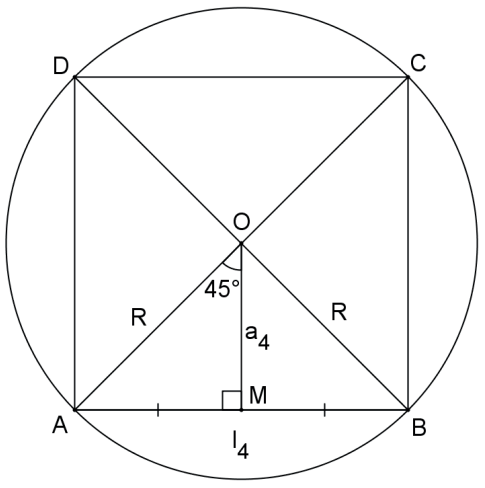
Demonstração:
No triângulo retângulo AOM da figura temos:
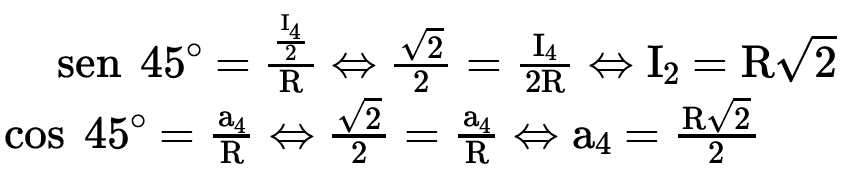
Poderíamos observar também que o triângulo da figura é um triângulo retângulo isósceles e, portanto, a4 =I4/2.
HEXÁGONO REGULAR CONVEXO INSCRITO
O lado de um hexágono regular convexo inscrito em uma circunferência de raio R é I6 = R e o seu apótema é a6 = a√3/2.
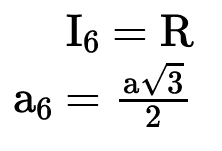
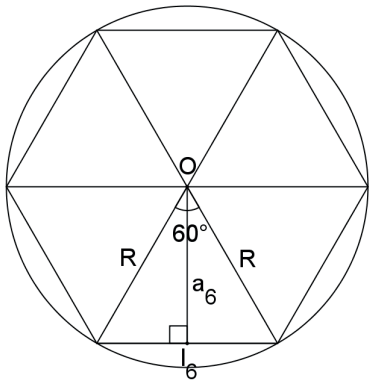
Demonstração:
O hexágono regular pode ser dividido em seis triângulos equiláteros. Dessa forma, o lado de cada triângulo equilátero é I6 = R e o apótema é igual à altura desse triângulo a6 = R√3/2.
TRIÂNGULO EQUILÁTERO CIRCUNSCRITO
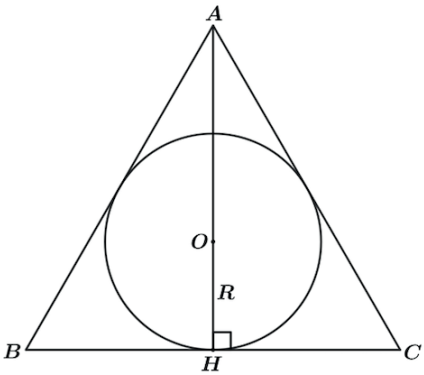
Pela razão de 2 : 1 do baricentro teremos que A̲O̲ = 2 O̲R̲ ⇒ A̲O̲ = 2R ⇒ A̲H̲ = 3R, assim:
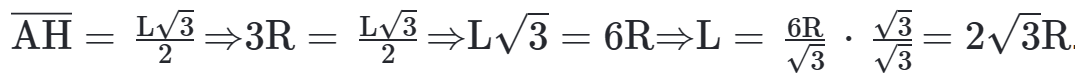
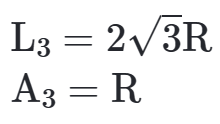
QUADRADO CIRCUNSCRITO
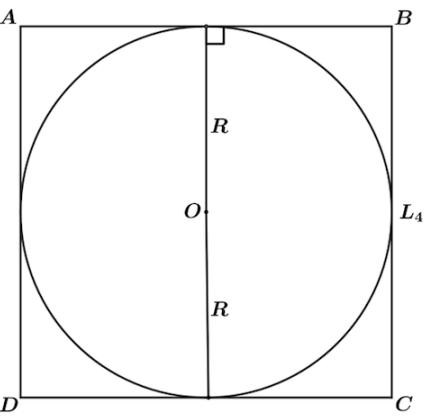
É fácil ver pela figura que L4 = 2R e A4 = R.
HEXÁGONO REGULAR CIRCUNSCRITO
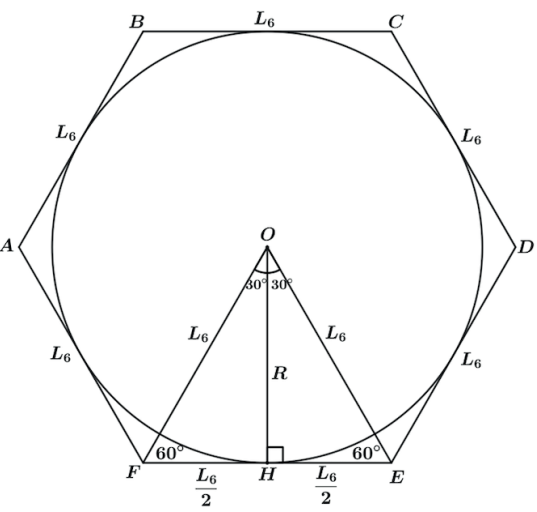
Podemos ver que o triângulo OEF é equilátero de lado L6 e altura R, assim teremos que: