REFRAÇÃO
É quando uma onda sofre uma mudança na sua velocidade devido à mudança do meio de propagação. A velocidade da luz no vácuo é 3 ⋅108 m/s; por sua vez, a velocidade da luz na água é na ordem de 2,2 ⋅ 108 m/s. No módulo de ondulatória, esse fenômeno é abordado de uma maneira mais detalhada. Por hora, o mais importante é entendermos que essa mudança na velocidade da luz pode causar um desvio do RL (falamos que ângulo de incidência é diferente do ângulo de refração; o ângulo entre o RL e a normal após mudança de meio de propagação).
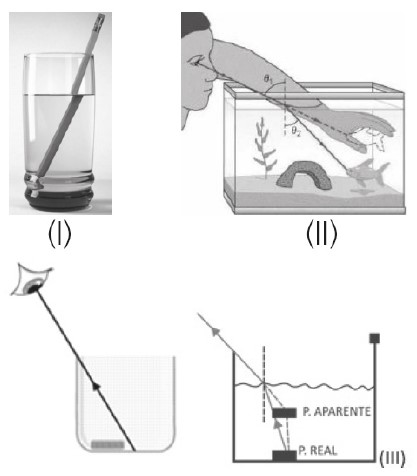
Na figura I, a refração faz com que o lápis aparente esteja quebrado. Ao ver com mais detalhes o que acontece quando observamos a figura II, a imagem formada do peixe para o menino está exatamente onde a sua mão se encontra, porém, como o RL sofre refração, o peixe está, na verdade, um pouco abaixo. É por isso que objetos no fundo de um copo com água aparentam estar um pouco acima de onde realmente estão. O mesmo vale para a profundidade de uma piscina. A distância entre a superfície de separação entre os meios e a posição onde a imagem se forma é chamada de altura aparente. A distância até onde o objeto de fato está é chamada de altura real.
Na figura III, antes de colocar água no copo, o observador não conseguia ver o objeto. Colocando água lentamente, o objeto passa a ser, aos poucos, visível. Note que, com o nível de água da figura, o observador verá a metade direita do objeto.
Abaixo temos, à esquerda, uma onda sonora (mecânica) e, à direita, um raio luminoso (onda eletromagnética), sofrendo refração ao sair do ar e entrar na água:
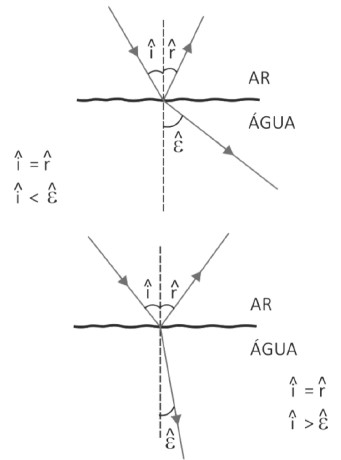
Perceba que, no primeiro caso, o vetor que indica a direção de propagação da onda se afasta da normal. Isso acontece porque o som é mais rápido na água que no ar.
Observação: Se o ângulo de incidência for 0°, ou seja, se o RL for normal à superfície de separação entre os meios, o ângulo de refração também será zero. Por isso, anteriormente afirmamos que, na refração, o RL pode ou não sofrer desvio. Para qualquer outro ângulo, havendo refração, haverá desvio do RL. A refração luminosa não é o desvio da luz, mas a mudança de velocidade da luz devido à mudança de meio de propagação, conforme dito no início do módulo.
Na segunda figura, o ângulo entre a direção de propagação e a normal diminui, já que a luz perde velocidade ao entrar na água.
Agora olhe o que acontece com os comprimentos de onda durante a refração:
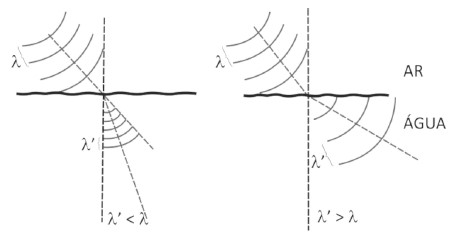
A frequência da onda não é alterada com a mudança de meio (uma luz vermelha não vai virar azul porque entrou na água, por exemplo). O comprimento de onda muda devido à mudança de velocidade. Sendo assim:

No caso específico da luz, dizemos que quanto maior o índice de refração do meio (n), menor será a sua velocidade de propagação.

Em que c é a velocidade da luz no vácuo, e v é a velocidade da luz no meio. Sendo assim, podemos comparar as velocidades de propagações nos meios através dos seus índices de refração:

Mas, o índice de refração nos diz mais que a velocidade da luz no meio. Também podemos descobrir a relação entre o ângulo de incidência e o ângulo de refração ε^ (apenas não utilizei a letra r, porque já a usamos para simbolizar o ângulo de reflexão dos RL):

Essa é a lei de Snell. A sua dedução também pode ser encontrada no livro de Moysés, citado anteriormente.
Sempre que um RL atinge uma superfície haverá refração? Não. Encontra-se, aqui, o detalhe. Se o RL atingir uma superfície com maior índice de refração, haverá, além da reflexão, refração. Porém, se o RL vier de um meio mais refringente e atingir a superfície de um meio menos refringente, pode ou não haver refração, mas haverá sempre reflexão. Se não houver refração, dizemos que haverá reflexão total. Mas, qual seria então essa condição? Como saber se haverá refração e reflexão ou só reflexão (reflexão total)?
Observe a figura abaixo:
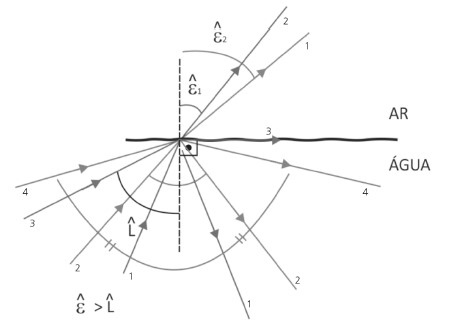
Quando o ângulo de incidência é igual a L^, o ângulo de refração vale 90°, ou seja, essa é a situação limite para haver refração. Qualquer RL que tenha ângulo de incidência superior a L^ não será refratado; será totalmente refletido. Chamamos L^ de ângulo limite.
Aplicando Snell:

Note que não há seno maior que 1. Logo, para haver reflexão total, n2 < n1.
Exercício Resolvido 1: Complete a direção do RL após refratar no prisma e calcule o ângulo que o RL fará com a normal ao abandoná-lo. Considere o índice de refração do prisma igual a 2.
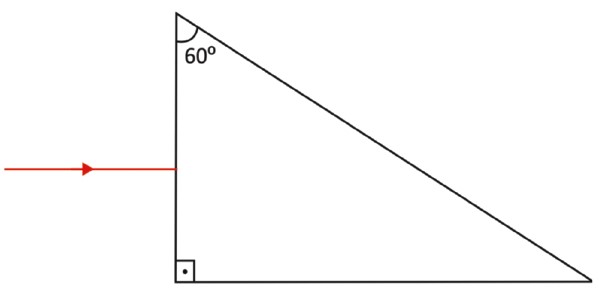
Resolução:
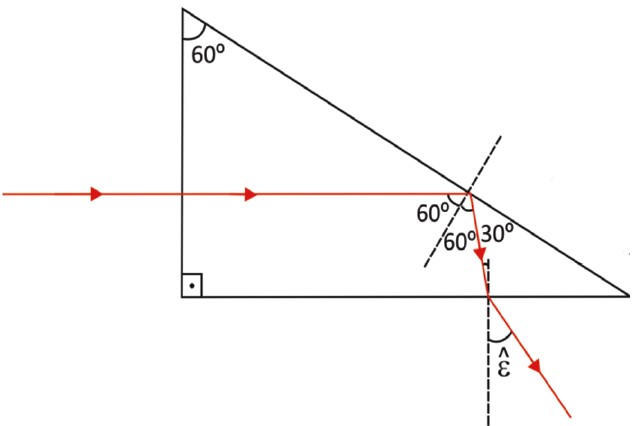

UM POUCO MAIS SOBRE REFRAÇÃO

Vimos anteriormente, nos nossos estudos de refração, que a frequência de uma onda não se altera quando o meio de propagação é alterado, mas o que deve acontecer com uma luz que não é monocromática, ou seja, uma luz com mais de uma frequência (cor), como a luz solar, por exemplo, quando muda de meio?
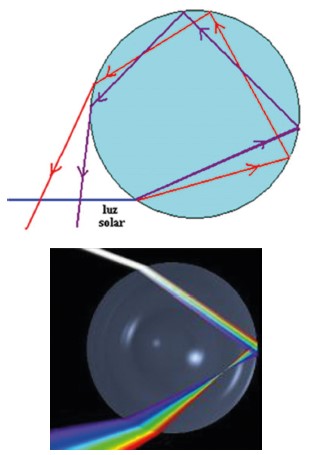
Esse fenômeno é conhecido como dispersão luminosa. A luz solar (luz branca), quando se propaga do ar para água, sofre dispersão, que nada mais é que a separação das luzes que a compõem, que são várias, mas podemos falar em 7 principais: Vermelho, Alaranjado, Amarelo, Verde, Azul, Anil e Violeta – VAAVAAV – sendo o vermelho a cor de menor frequência (portanto, maior comprimento de onda) e o violeta, a cor com maior frequência (menor comprimento de onda).
A dispersão foi observada por Newton, em 1666, quando deixou a luz do Sol incidir em um prisma. Seu estudo foi publicado no seu livro de tratado da óptica.
No vácuo, uma luz monocromática vermelha possui a mesma velocidade que uma violeta, por exemplo. Não importa a cor (frequência). A velocidade de qualquer luz (na verdade, de qualquer onda eletromagnética, como o rádio, raio-X etc) no vácuo é igual a c (3 ⋅ 108 m/s). Porém, em outro meio, como a água, a velocidade de cada frequência é diferente e é justamente isso que faz a dispersão acontecer.
Veja a figura abaixo. Um feixe de luz branca está indo do ar para água. Na dispersão, a luz com maior velocidade (vermelho) se afasta da normal, obedecendo ao princípio da refração e, a mais lenta (violeta), será mais próxima da normal.
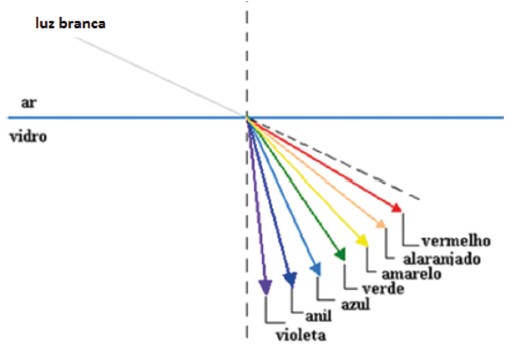
Um prisma funciona como a água nesse caso, fazendo a luz sofrer dispersão:
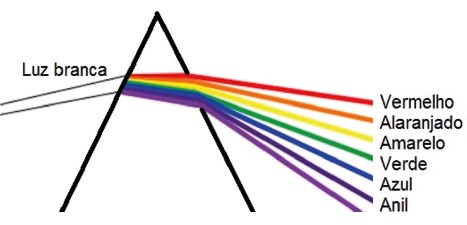
Mas, e se a luz branca estiver saindo da água (ou de um prisma) e indo para o ar?
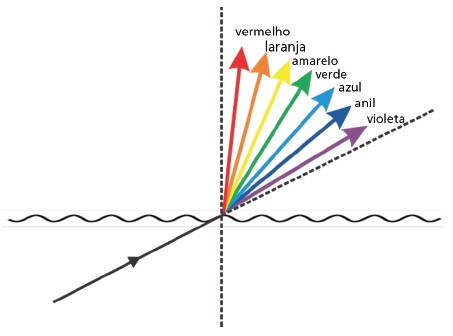
Note pela figura acima que, pela equação de Snell, temos uma inversão em relação à dispersão ar-água. Nesse caso, o vermelho tende a se aproximar mais da normal que o violeta.
Com isso conseguimos entender um dos fenômenos mais belos da natureza, o arco-íris. As gotículas de água em suspensão no ar funcionam como pequenos prismas. A luz do Sol, ao penetrar nessas gotículas, sofre dispersão, como podemos ver com mais detalhes na figura abaixo: