ÍNDICE DE REFRAÇÃO
No vácuo, todas as ondas eletromagéticas se propagam com a mesma velocidade, no entanto ao mudarem de meio cada uma dessas ondas possui uma velocidade diferente e menor que no vácuo devido à interação dessas ondas com a matéria.
Observação: essa transição de meio é chamada de refração e além da velocidade, o comprimento de onda também muda, mas a sua frequência permanece constante.
O índice de refração (n) ou refringência de um meio é uma grandeza física adimensional dada por:

Onde:
- v é a velocidade da luz no meio
- c é a velocidade da luz no vácuo
– Consideramos a velocidade da luz no ar como muito próxima à do vácuo, portanto nar = 1.
– Para qualquer outro meio: v<c, então nmeio>1.
LEIS DE REFRAÇÃO
Durante a refração, a luz pode sofrer algumas alterações na sua trajetória, ocasionando diversos fenômenos facilmente observados como a posição aparente de um objeto no interior de um copo com água.

Posição aparente de um lápis dentro d’água devido à refração
Vamos determinar a trajetória seguida por um raio de luz monocromático que se propagando num meio 1 passa a se propagar num meio 2.
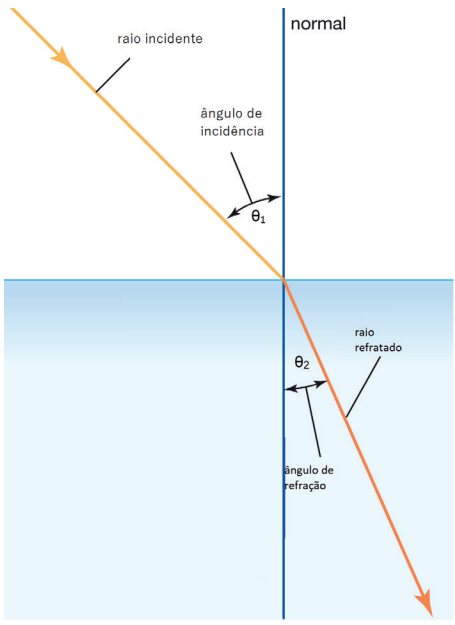
Trajetória dos raios luminosos na refração
- 1ª Lei da Refração: o raio incidente, refletido, refratado e a reta normal são coplanares.
- 2ª Lei da Refração: A relação ente os ângulos de incidência (θ1) e refração (θ2) é dada pela lei de Snell:

TIPOS DE INCIDÊNCIA
Vamos agora analisar os possíveis resultados derivados da lei de Snell:
INCIDÊNCIA OBLÍQUA (n2 > n1)
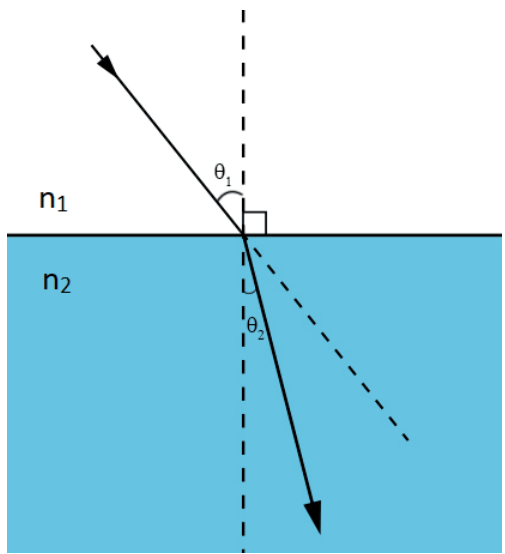
Trajetória dos raios luminosos na refração
Observação: quando o raio de luz incide obliquamente em um dioptro indo meio menos refringente para o meio mais refringente, ele se aproxima da reta normal ou se afasta da superfície.
n1 · sen (θ1) = n2 · sen (θ2)
n1 < n2 ⇒ θ1 > θ2
INCIDÊNCIA OBLÍQUA (n2 < n1)
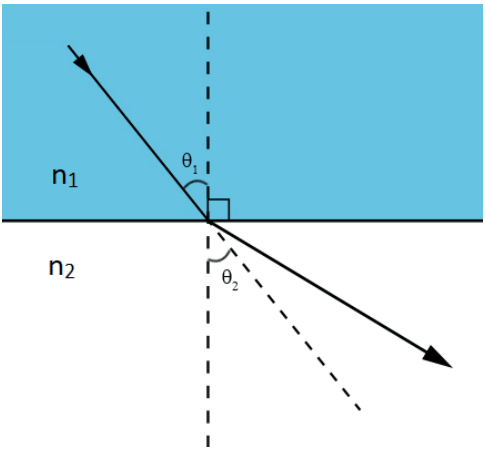
Observação: quando o raio de luz incide obliquamente em um dioptro indo meio mais refringente para o meio menos refringente, ele se afasta da reta normal ou se aproxima da superfície.
n1 · sen (θ1) = n2 · sen (θ2)
n1 > n2 ⇒ θ1 < θ2
INCIDÊNCIA NORMAL (∀n1, n2)
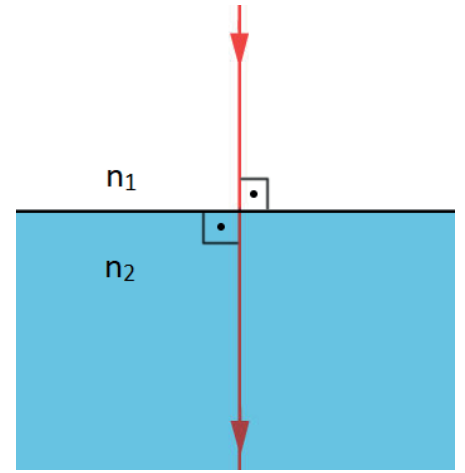
Observação: quando o raio de luz incide perpendicularmente à superfície ou paralelamente à normal em um, ele não sofre desvio na sua trajetória.
n1 · sen (θ1) = n2 · sen (θ2)
θ1 = 0 ⇒ θ2 = 0
Exemplo: em uma estação, um cartaz informativo está protegido por uma lâmina de material transparente. Um feixe de luz monocromático, refletido pelo cartaz, incide sobre a interface de separação entre a lâmina e o ar, formando com a vertical um ângulo de 53°. Ao se refratar, esse feixe forma um ângulo de 30° com a mesma vertical. Observe o esquema ampliado a seguir, que representa a passagem do raio de luz entre a lâmina e o ar.
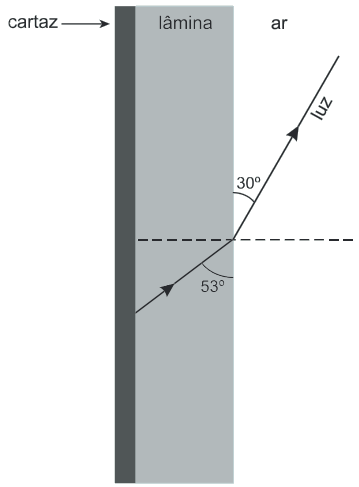
Determine o índice de refração da lâmina.
Resolução:
Aplicando a lei de Snell, temos:
nar · sen (90° – 30°) = nlammina · sen (90° – 53°)
1·0,87 = nlâmina · 0,6 ∴ nlâmina = 1,45
REFLEXÃO TOTAL
Observe no caso de incidência oblíqua em que o raio se afasta da normal. Se aumentarmos o ângulo de incidência, o ângulo de refração também aumentará. Contudo, há um limite para esse último crescer. A partir desse limite, o raio incidente não sofrerá mais refração, tendo toda a sua energia refletida pelo dioptro. Chamamos esse fenômeno de reflexão total.
Para determinarmos qual o ângulo máximo de incidência, chamado de de ângulo limite (L), usaremos a Lei de Snell com a refração valendo 90º, ou seja, o raio “sai” rasante ao dioptro.
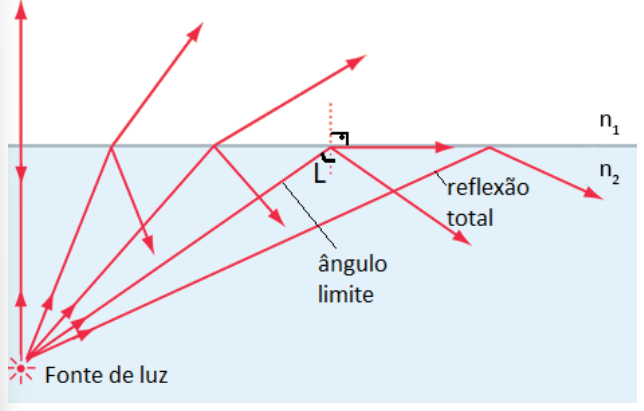
Ângulo limite de refração

Observação:
- Na prática, esse raio rasante não existe. O raio sofre refração ou reflexão total.
- Só pode haver reflexão total quando o raio vai do meio mais para o meio menos refringente.
Exemplo:
Uma das mais importantes aplicações da reflexão total é a fibra óptica, usada na transmissão de dados e comunicação. A informação é propagada na forma de luz através de tubos transparentes com grandes ângulos de incidência de forma que o raio sofra múltiplas reflexões totais até emergir na outra ponta
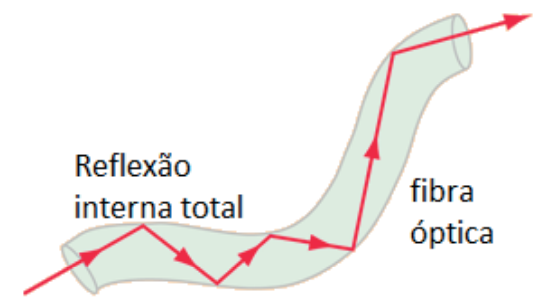
Trajetória do raio luminoso na fiba óptica
MIRAGEM
Nossos olhos são incapazes de enxergar o desvio que pode ser causado durante a refeação. Eles sempre veem os raios de luz se propagando em linha reta, por isso podemos observar várias imagens estranhas sendo formadas como a miragem e a fata morgana.
A atmosfera terrestre não é homogênea e, portanto, o índice de refração pode variar com a altura e a temperatura. Quando a temperatura do solo é elevada, o ar aquecido junto ao solo fica menos refringente e a luz sofre refrações sucessivas no próprio ar atmosférico.
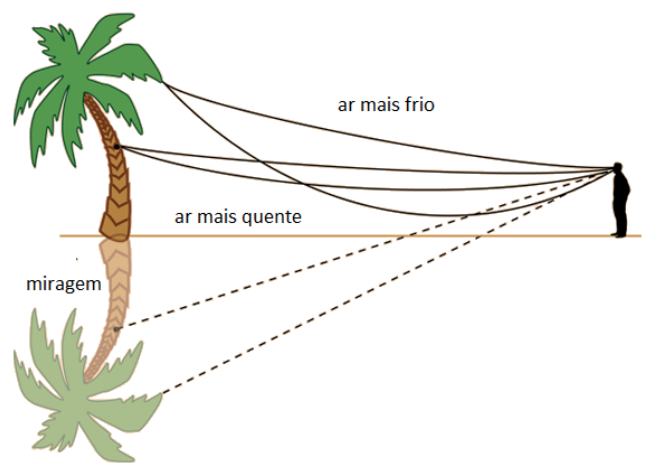
Refração na atmosfera
Pelo mesmo motivo, temos a impressão de que as estradas num dia muito quente estão molhadas quando observadas convenientemente.

Pista aparentemente molhada devido à refração na atmosfera
Caso a temperatura próxima à superfície da água seja muito baixa, o ar mais frio se torna mais refringente e a luz sofre refrações sucessivas no próprio ar atmosférico ao contrário da miragem, conhecido como fata morgana. A imagem abaixo ilustra tal fenômeno em que o navio parece estar voando sobre a água.

Fenômeno da fata morgana
Curisiodade: acredita-se que a lenda do holandês voador, um navio amaldiçoado, tenha surgido devido à observação do fenômeno da fata morgana.
DIPOTRO PLANO
Conforme já verificamos, observar objetos após a refração nos faz enxergar a imagem em uma posição diferente da que ele realmente se encontra. Vamos usar as leis de refração para determinarmos as características das imagens formadas pelos dioptros planos, superfícies que separam dois meios com índices de refração diferentes cuja fronteira é plana.
OBJETO NO MEIO MAIS REFRINGENTE E OBSERVADOR NO MEIO MENOS REFRINGENTE
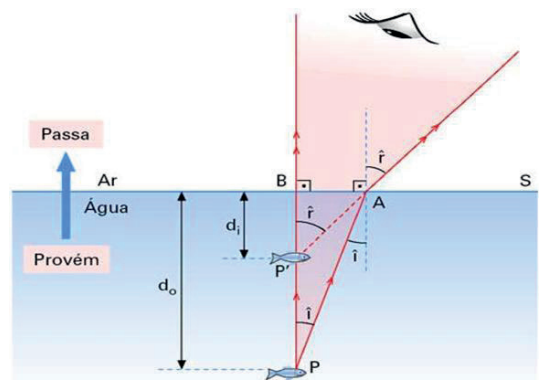
Observe dois raios que partem de um objeto no interior da água para os olhos de um observador que se encontra no ar. Ao fazermos o prolongamento dos raios refratados, percebemos que a imagem está mais próxima da superfície que o objeto.
Observação: cuidado ao pular numa piscina, pois, devido à refração, ela parece mais rasa.
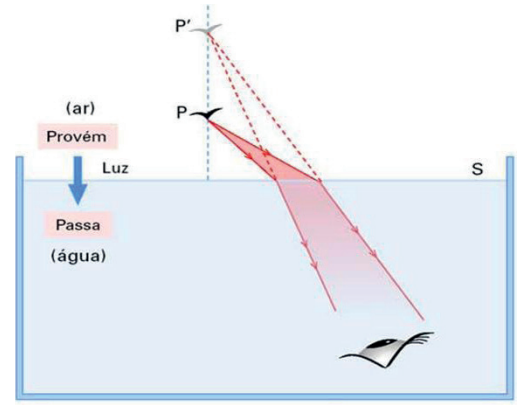
OBJETO NO MEIO MENOS REFRINGENTE E OBSERVADOR NO MEIO MAIS REFRINGENTE
Se agora tivermos o observador dentro da água enxergando um objeto do lado de fora, a imagem será vista mais afastada da superfície que o objeto.
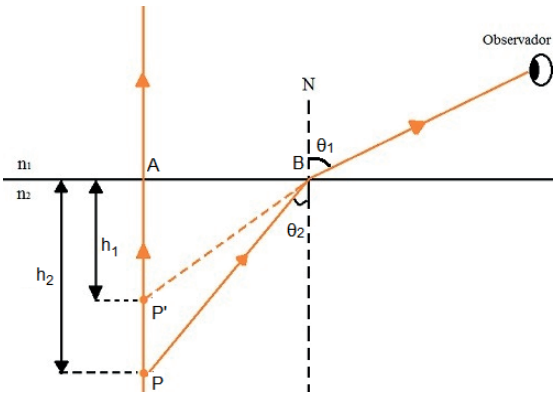
EQUAÇÃO DO DIOPTRO PLANO
Vamos mais uma vez utilizar a aproximação gaussiana, ângulos muito pequenos, para realizarmos nossos cálculos e determinarmos a posição da imagem.
Pela Lei de Snell:
n1 · sen (θ1) = n2 · sen (θ2)
Como o ângulo de incidência é muito pequeno, podemos usar a seguinte a aproximação:
sen (θ1) = tan (θ1) = θ1
Voltando à lei de Snell e achando as tangentes dos triângulos ABP e ABP’, temos:

LÂMINAS DE FACES PARALELAS
Considere agora o trajeto da luz ao passar pelo vidro da sua janela, por exemplo. Ele passa do ar para o vidro e depois de volta para o ar. Se os dioptros forem planos e paralelos, haverá um desvio lateral na trajetória dos raios luminosos como representado na figura abaixo:
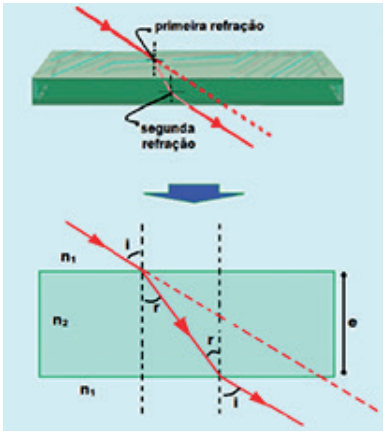
Luz atavessando uma lâmina de faces paralelas
Vamos calcular o deslocamento d sofrido pelo raio ao atravessar uma lâmina de espessura e.
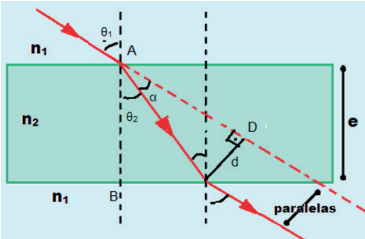

Observação: uma aproximação muito usada é para ângulos pequenos. Nesse caso,
sen (θ1 – θ2) = θ1 – θ2 e cos (θ2) = 1. Usando a lei de Snell, temos a relação entre os ângulos:

PRISMAS
Para lâminas planas de faces não paralelas, conhecido como prisma, o raio de luz sofrerá um desvio angular.
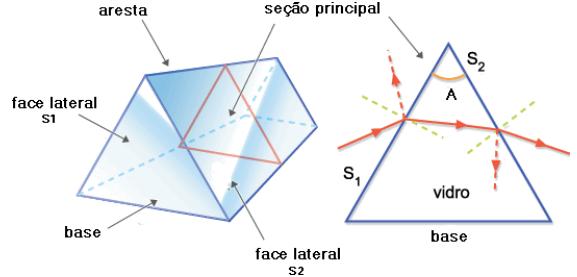
Secção reta de um prisma
Esse desvio δ pode ser calculado por meios puramente geométricos como observado a seguir.
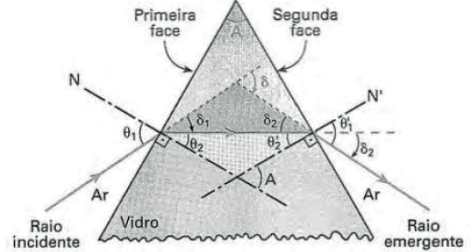
Desvio do raio luminoso ao atravessar um prisma
- O ângulo de abertura do prisma A é ângulo externo e portanto vale A = θ2 + θ2′
- Na primeira refração, o raio passa do ar para o prisma e se aproxima da primeira normal N1, sofrendo um desvio δ1 = θ1 – θ2.
- Na segunda refração, o raio sai do prisma para o ar e se afasta da normal N2, sofrendo um desvio δ2 = θ‘1 – θ‘2.
- O desvio total sofrido pelo raio luminoso será a soma desses desvios, ou seja, δ = δ1 + δ2.
δ = (θ1 – θ2) + (θ‘1 – θ‘2)
δ = (θ1 + θ‘1) – (θ2 + θ‘2)
δ = (θ1 + θ‘1) – A
Observação: a segunda refração pode não ocorrer, caso haja reflexão total nessa face. Há uma condição em que o desvio do raio luminoso é o mínimo, quando θ1 = θ‘1. δmin = 2θ1 – A
Observação: mais uma vez, podemos usar a aproximação gaussiana para calcular o desvio para ângulos pequenos. Lembrando que nesse caso a lei de Snell será da forma

DISPERSÃO DA LUZ
A luz policromática pode ser decomposta nas diversas cores que a compõem durante a refração, porque cada cor (frequência) possui índice de refração diferente e sofrerá desvios distintos ao atravessar um dioptro. Esse fenômeno é denominado dispersão.

Dispersão da luz em um prisma
Observação Quando maior a frequência da onda, maior é o seu índice de refração e mais desvio esse raio sofrerá na refração. Assim, podemos analisar os extremos do espectro visível nvioleta > nvermelho .
FORMAÇÃO DO ARCO-ÍRIS

O arco-íris é um fenômeno natural que ocorre devido à dispersão da luz nas gotas de água presentes na atmosfera. A luz branca penetra a gota, decompondo-se em infinitos espectros, e sofre reflexão total para ângulos próximos a 40°, sendo refletida para um observador de costar para o sol.
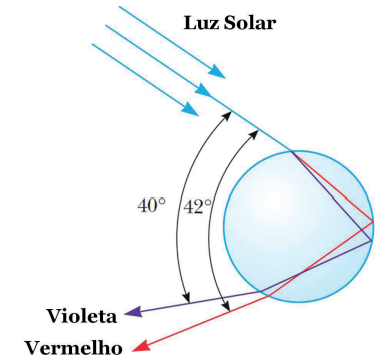
Dispersão e reflexão da luz solar dentro de uma gota
Observação Caso você tente perseguir um arco-íris, ele irá se afastar de você, mantendo-se sempre a um ângulo fixo no céu.




