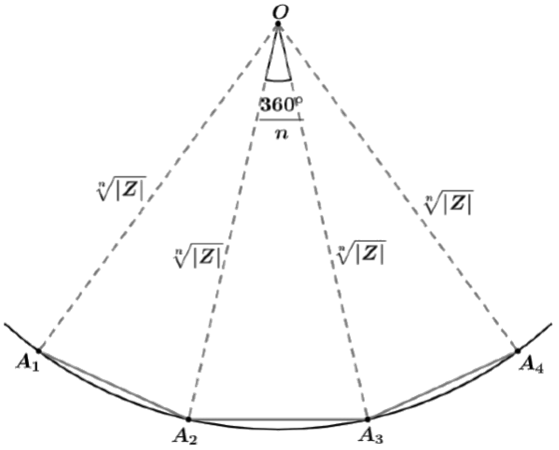
A parte mais brilhante do estudo talvez se dê agora. A representação das raízes complexas no plano de Argand-Gauss (A patir da raíz de índice 3) sempre resulta em um polígono regular. Vimos que sempre que fazemos a radiciação de um número complexo temos que

Se lembrarmos da geometria plana, mais precisamente do estudo dos polígonos regulares, lembraremos que para qualquer polígono regular 360°/n representa o seu ângulo central.
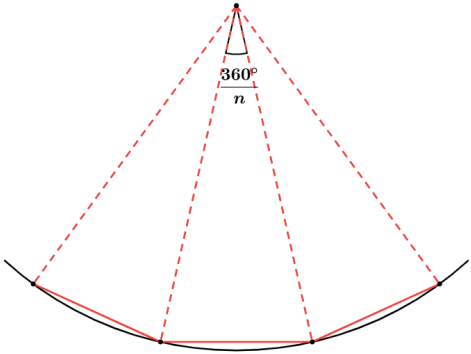
Dessa maneira sempre que executamos a radiciação de um número complexo, no plano de Argand-Gauss teremos formado um polígono regular.
Quando fazemos a raiz cúbica temos o triângulo equilátero, quando fazemos a raiz quarta temos o quadrado e assim por diante.
Sabendo disso, não a necessidade de substituirmos o k por 0, por 1, … na operação de radiciação. Basta fazermos somente k=0 e depois somarmos o valor do ângulo central do nosso polígono regular no argumento encontrado para k=0 até que encontremos todas as raízes.
No exemplo anterior, quando encontramos

bastava sabermos que essas raízes, quando representadas no plano, iriam gerar um quadrado e dessa forma basta somar 90° em cada argumento a partir do argumento 60°, assim

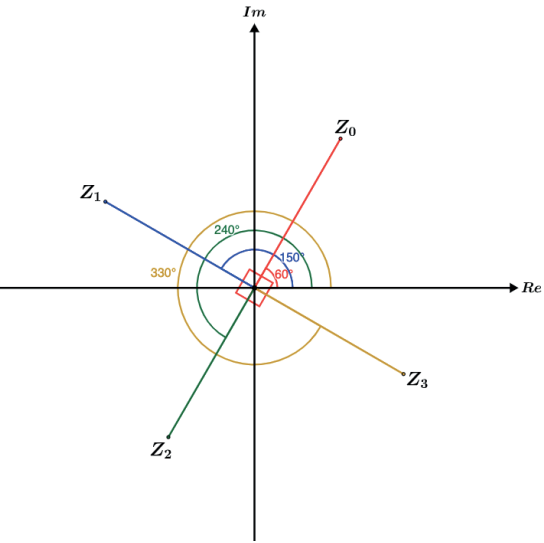
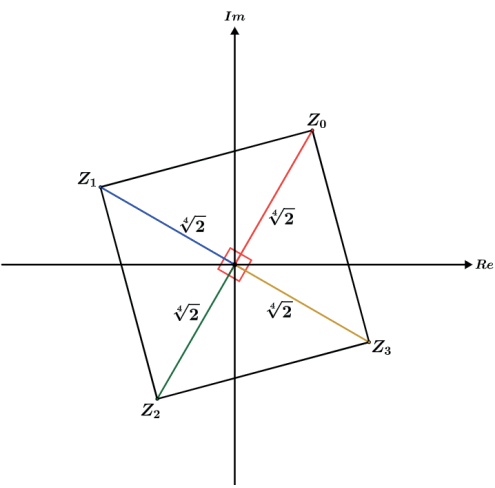
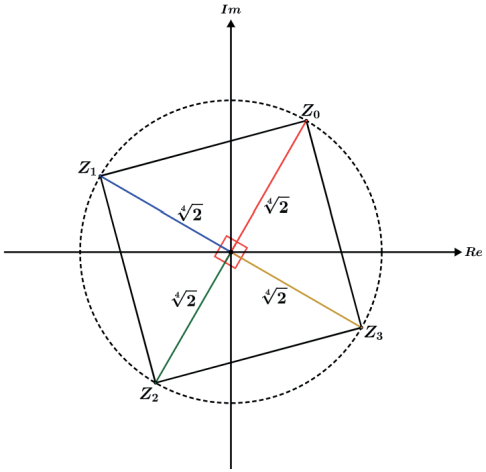
O polígono sempre será inscrito numa circunferência de raio
ProBizu
Muitas questões nos pedem a área do polígono gerado pelas raízes n-ésimas de um complexo. Vamos definir uma fórmula bem simples, que inclusive não depende das raízes mas sim somente de: