Progressão geométrica

Veja a história a seguir:

“O grão-vizir, principal conselheiro do rei, tinha inventado um novo jogo. Era jogado com peças móveis sobre um tabuleiro quadrado que consistia em 64 quadrados vermelhos e pretos. O objetivo era capturar o rei inimigo, e por isso o jogo era chamado, em persa, shahmat – shah para rei, mat para morto. Morte ao rei. O jogo, claro, é o xadrez. Mas reza a história que o rei ficou tão encantado com a invenção que mandou o grão-vizir determinar sua própria recompensa. O grão-vizir já tinha a resposta na língua: era um homem modesto, disse ao xá. Desejava apenas uma recompensa simples. Apontando as oito colunas e as oito filas de quadrados no tabuleiro que tinha inventado, pediu que lhe fosse dado um único grão de trigo no primeiro quadrado, o dobro dessa quantia no segundo, o dobro dessa quantia no terceiro e assim por diante, até que cada quadrado tivesse o seu complemento de trigo. Não protestou o rei, era uma recompensa demasiada modesta para uma invenção tão importante.

No entanto, quando o mestre do Celeiro Real começou a contar os grãos, o rei se viu diante de uma surpresa desagradável. O número de grãos começa bem pequeno: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024… mas quando se chega ao 64° quadrado, o número se torna colossal, esmagador. O número final chega a quase 18,5 quintilhões (se cada grão tivesse o tamanho de um milímetro, todos os grãos juntos pesariam cerca de 75 bilhões de toneladas!).”

Este é um exemplo de progressão geométrica, que é o assunto que estudaremos a seguir.

Exemplos:

I. 1, 1, 1, 1, 1 é uma progressão geométrica com 5 termos e cuja razão é igual a ¹/₁ =1.
II. 1, 2, 4, 8, 16 é uma progressão geométrica infinita com razão 2.
III. 1, − ¹/₂ , ¹/₄ , − ¹/₈ , ¹/₁₆ , − ¹/₃₂é uma progressão aritmética com 6 termos e cuja razão é − ¹/₂.

CLASSIFICAÇÃO

CRESCENTES

Uma progressão geométrica é crescente quando o termo subsequente é maior que o termo anterior.

a_n+1 > a_n

Caso 1: a₁ > 0

Para que uma P.G. de primeiro termo positivo seja crescente devemos ter q > 1.

Caso 2: a₁ < 0

Para que uma P.G. de primeiro termo negativo seja crescente devemos ter 0 < q < 1.

Exemplos:

(2, 6, 18, 54, …) é uma P.G. crescente pois o primeiro termo é positivo (a₁ = 2) e a razão é maior que 1 (q = 3).

(−4,−2,−1, − ¹/² , − ¹/₄ , …) é uma P.G. crescente pois o primeiro termo é negativo (a1 = -4) e a razão é um número compreendido entre 0 e 1 (q = ¹/₂).

DECRESCENTES

Uma progressão geométrica é decrescente quando o termo subsequente é menor que o termo anterior.

a_n+1 < a_n

Caso 1: a₁> 0

Para que uma P.G. de primeiro termo positivo seja decrescente devemos ter 0 < q < 1.

Caso 2: a1<0

Para que uma P.G. de primeiro termo negativo seja decrescente devemos ter q > 1.

Exemplos:

(18, 6, 2, ²/₃ , …) é uma P.G. decrescente pois o primeiro termo é positivo (a₁ = 18) e a razão está entre 0 e 1 (q = ¹/₃ ).

(−1,−2,−4,−8,−16, …) é uma P.G. decrescente pois o primeiro termo é negativo (a1 = -1) e a razão é maior que 1 (q = 2).

ALTERNANTES

Uma progressão geométrica é alternante quando o termo subsequente possui o sinal contrário do termo anterior.

a_n+1 ⋅ a_n < 0

Para que uma P.G. seja alternante basta que a sua razão seja negativa (q < 0).

Exemplo:

(3,−6, 12,−24, 48, …) é uma P.G. alternante pois a sua razão é negativa (q = -2).

CONSTANTE

Uma progressão geométrica é constante quando todos os termos são iguais.

a_n+1 = a_n

Para que uma P.G. seja constante basta que a razão seja igual a 1 ou o caso particular de primeiro termo igual a 0 e qualquer razão.

Exemplo:

(4, 4, 4, 4, 4, …) é uma P.G. constante pois a razão é igual a 1 q=1.

(0, 0, 0, 0, …) é uma P.G. constante e não é possível determinarmos a razão.

A P.G. (0, 0, 0, 0, …) é chamada de P.G. constante de razão indeterminada.

ESTACIONÁRIA

Uma progressão geométrica é estacionária quando sua razão é igual a 0 (q = 0) e o primeiro termo é diferente de 0 (a₁ ≠ 0).

(4, 0, 0, 0, 0, …) é uma P.G. estacionária pois q = 0 e a₁ = 4.

TERMO GERAL

Vamos deduzir agora fórmulas para encontrar um termo de uma PG se conhecermos outro termo e a razão.

N-ÉSIMO TERMO EM FUNÇÃO DO PRIMEIRO

Podemos escrever:

Multiplicando todas as equações e cancelando os termos, obtemos:

a_n = a₁qⁿ⁻¹

N-ÉSIMO TERMO EM FUNÇÃO DO P-ÉSIMO

Com um procedimento análogo ao do item anterior, podemos deduzir que:

a_n= a_pq^n−p

Veja que esta fórmula permite relacionar quaisquer dois termos de uma PG. Além disso, a fórmula deduzida em I é um caso particular desta.

INTERPOLAÇÃO GEOMÉTRICA

Interpolar, inserir ou intercalar k meios geométricos entre os extremos a e b significa construir uma progressão geométrica de k + 2 termos, sendo que o primeiro termo é igual a a e o segundo termo é igual a b.

Vejamos um exemplo:

Intercalar 8 meios geométricos entre os extremos 5 e 2560.

Solução:

Queremos construir uma PG a₁, a₂, …, a₁₀ de forma que a₁ = 5 e a₁₀ = 2560. Com base nisto, vamos determinar a razão q da PG: pela fórmula do termo geral, temos que a₁₀ = a1 · q⁹ . Substituindo a₁ = 5 e a₁₀ =2560, segue que 2560 = 5 · q⁹ ⇔ q⁹ = 512 ⇔ q = 2. Desta forma, os meios que devemos inserir são:

10, 20, 40, 80, 160, 320, 640, 1280

SOMA DOS TERMOS DE UMA PG FINITA

Agora, estaremos interessados em calcular a soma dos termos de uma progressão geométrica:

S_n = a₁ + a₂ +…+ a_n − 1 + a_n

Utilizando a fórmula do termo geral, podemos reescrever

S_n = a₁ + a₁q + a₁q² +…+ a₁qⁿ⁻¹ (1)

O truque agora é multiplicar ambos os lados pela razão q, obtendo assim:

S_nq = a₁q + a₁q² + a₁q³ +…+ a₁qⁿ (2)

Fazendo (2) – (1), obtemos, após cancelar os termos comuns:

S_n(q−1) = a₁ · (qⁿ − 1)

Supondo q ≠ 1, obtemos a seguinte fórmula:

Por outro lado, se q = 1, todos os termos da PG são iguais ao primeiro e obtemos:

S_n = n · a₁

PRODUTO DOS TERMOS DE UMA PG

Estamos agora interessados em calcular P_n = a₁ · a₂ · … · a_n. Substituindo a₂ , a₃ , …, a_n pelas expressões obtidas através do termo geral, temos: Pn = a₁ ⋅ a₁q ⋅ a₁q² ⋅…⋅ a₁qⁿ⁻¹.

Logo obtemos:

MA DOS TERMOS DE UMA PG INFINITA

Consideraremos agora PG’s infinitas cuja razão q é tal que |q| < 1, ou seja, –1 < q < 1. Estamos interessados em calcular S = a₁ + a₂ +… + a_n +…. Para isso, note que as somas S_n = a₁ + a₂+…+ a_n se aproximam cada vez mais de S, quando n vai ficando cada vez maior. Pela fórmula da soma dos termos de uma PG finita, temos que S_n = ^a1·(qn−1)/_(q−1). Repare agora que quando n fica cada vez maior, temos que q_n se aproxima cada vez mais de 0. Formalmente, temos que:

Com isso, obtemos a seguinte fórmula para a soma dos termos de uma PG infinita:

Observação: Para três termos consecutivos a, b, c de uma PG, vale que b² = a · c.

PROGRESSÃO ARITMÉTICAGEOMÉTRICA (PAG)

DEFINIÇÃO

Uma PAG é uma sequência cujo termo geral é da forma a_n = u_nv_n , onde u_n é uma progressão aritmética e v_n é uma progressão geométrica. Vejamos alguns exemplos para esclarecer a definição.

Exemplos:

I. 1⋅1, 2⋅2, 3 ⋅ 4, 4 ⋅ 8, 5 ⋅ 16,… é uma PAG, pois seus termos são os produtos dos termos da PA 1, 2, 3, 4, 5, … pelos termos da PG 1, 2, 4, 8, 16, …

II.

é uma PAG, pois seus termos são os produtos dos termos da PA 3, 6, 9, 12, 15 pelos termos da PG:

SOMA DOS TERMOS DE UMA PAG

Não desenvolveremos aqui uma fórmula geral para o cálculo da soma dos termos de uma PAG, pois não é de grande valia guardar esta fórmula. O mais importante, na verdade, é saber o procedimento para se calcular a soma dos termos de uma PAG. Este procedimento é completamente similar ao método utilizado para o cálculo da soma dos termos de uma PG.

Observação: A ideia que deve ser gravada é: para calcular a soma dos termos de uma PAG, multiplique a soma desejada pela razão da PG e subtraia as duas relações encontradas.

Vejamos um exemplo para que as coisas fiquem ainda mais claras:

Solução:

Esta é a soma de uma PAG infinita. Para calcular esta soma, multiplicaremos S inicialmente pela razão da PG, que é 1/3. Assim, obtemos:

Fazendo (2) – (1), obtemos:

Caímos agora na soma dos termos de uma PG infinita de termo inicial 1/3 e razão 1/3. Assim, usando a fórmula da soma dos termos de uma PG infinita, temos:

PROGRESSÕES DE ORDEM SUPERIOR

Considere a seguinte imagem:

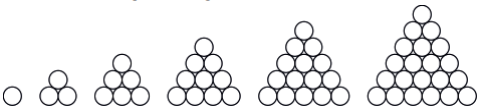
Contando o número de bolinhas em cada figura, temos:

Figura 1 – 1 bolinha
Figura 2 – 3 bolinhas
Figura 3 – 6 bolinhas
Figura 4 – 10 bolinhas
Figura 5 – 15 bolinhas
Figura 6 – 21 bolinhas

A sequência do número de bolinhas em cada figura é dada por 1, 3, 6, 10, 15, 21.

Agora, vamos observar as diferenças entre o número de bolinhas entre uma figura e a próxima:

3−1=2
6−3=3
10−6=4
15−10=5
21−15=6

Veja que a sequência formada por estas diferenças constitui uma progressão aritmética. Pela definição que veremos a seguir, a sequência do número de bolinhas em cada figura constituirá uma progressão aritmética de segunda ordem.

Observação: Os números desta sequência que consideramos são chamados de números triangulares.

DEFINIÇÃO

A definição de uma PA de ordem superior é recursiva, ou seja, a definição depende das definições anteriores. Começaremos definindo o que é uma PA de 2ª ordem, depois o que é uma PA de 3ª ordem e em seguida generalizaremos a definição.

1. PA de 2ª ordem: uma sequência é dita uma PA de segunda ordem se as diferenças entre seus termos consecutivos constituem uma PA.

Exemplos:

a) 1, 3, 6, 10, 15, 21, 28 é uma PA de segunda ordem, pois as diferenças entre os termos consecutivos formam a sequência 2, 3, 4, 5, 6, 7, que é uma PA.
b) 1, 3, 7, 13, 21, 31 é uma PA de segunda ordem, pois as diferenças entre os termos consecutivos formam a sequência 2, 4, 6, 8, 10, que é uma PA.

2. PA de 3ª ordem: uma sequência é dita uma PA de segunda ordem se as diferenças entre seus termos consecutivos constituem uma PA de segunda ordem.

Exemplos:

c) 1, 8, 27, 64, 125, 216 é uma PA de terceira ordem, pois as diferenças entre os termos consecutivos formam a sequência 7, 19, 37, 61, 91, que é uma PA de segunda ordem, uma vez que as diferenças entre os termos consecutivos desta última sequência são 11, 18, 24, 30, que é uma PA.

3. PA de k-ésima ordem: uma sequência é dita uma PA de ordem k se as diferenças entre seus termos consecutivos constituem uma PA de ordem k – 1.

TERMO GERAL

Não demonstraremos o resultado a seguir neste material, pois a demonstração foge ao escopo dos concursos para os quais estamos nos preparando (a prova utiliza indução forte e algumas manipulações algébricas).

TEOREMA 1: O termo geral de uma PA de ordem k é um polinômio de grau k.

SOMA DOS TERMOS

Mais uma vez, não demonstraremos o resultado a seguir.

TEOREMA 2: A soma dos termos de uma PA de ordem k é um polinômio de grau k + 1, sem termo independente.

TERMO GERAL DE UMA P.A. DE 2ª ORDEM

Vamos definir o operador diferença (Δa_n) = a_n+1 − a_nque será uma nova sequência e (Δ²a_n) = a_n+1 – a_n da nova sequência encontrada.

(3, 7, 13, 21,…) ⇒ (Δa₁) = 7− 3 = 4, (Δa₂) =13 − 7 = 6 e (Δa₃) = 21 − 13 = 8

Resultando na nova sequência (4, 6, 8,…) que é uma PA. Aplicando Δ²a_n teremos

(4, 6, 8, 10, …) ⇒ (Δ²a₁) = 6 − 4 = 2, (Δ²a₂) = 8 − 6 = 2 e (Δ²a₃) = 2

Assim teremos a PA constante (2, 2, 2, 2, …) de onde concluímos que (3, 7, 13, 21,…) é uma P.A. de 2ª ordem. Assim podemos definir a fórmula.