EVENTO
Subconjunto do espaço amostral do experimento.
Notação: A, B, C, …
𝛟 (conjunto vazio): evento impossível.
Ω: espaço amostral
Exemplo: lançamento de um dado.
Espaço amostral: Ω ={1,2,3,4,5,6}
Alguns eventos:
A: sair face par
B: Sair face maior que 3
C: Sair face 1
A ={2, 4, 6} ⇒ ⊂ Ω
B ={4, 5, 6} ⇒ ⊂ Ω
C ={1} ⇒ ⊂ Ω
OPERAÇÕES COM EVENTOS
INTERSEC̣ÃO
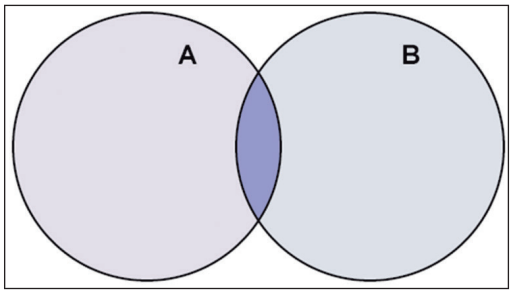
O evento interseção de dois eventos A e B equivale à ocorrência de ambos.
Notação: A ∩ B
EVENTOS MUTUAMENTE EXCLUSIVOS
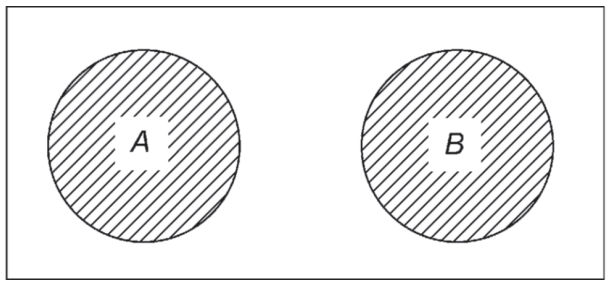
Dois eventos A e B dizem-se mutuamente exclusivos, ou mutuamente excludentes, quando a ocorrência de um deles impossibilita a ocorrência do outro.
Exprime-se este fato escrevendo-se A ∩ B =∅.
UNIÃO
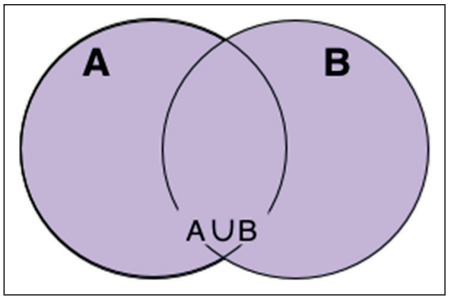
O evento união de A e B equivale à ocorrência de A, ou de B, ou ambas.
Notação: A ∪ B
COMPLEMENTAR
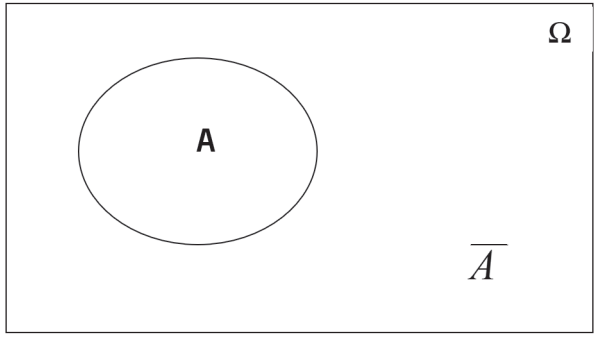
A negação do evento A, denotado por A̲, é chamado de evento complementar de A.
A e A̲ são complementares se sua intersecção é vazia e sua união é o espaço amostral, isto é,
A ∩ A̲ = ∅ e A ∪ A̲ = Ω
PROBABILIDADE DE UM EVENTO
É uma função que atribui um número aos eventos que pertence ao espaço amostral (se A é um evento de Ω,P(A) é a probabilidade de A), que satisfaz as seguintes condições:
0 ≤ P (A) ≤1,∀A ⊂ Ω
P(Ω)=1;
Se A e B são eventos mutuamente excludentes, então P(A ∪ B) = P(A) + P(B).
TEOREMAS FUNDAMENTAIS
P(∅)=0
P(A̲)=1-P(A)
Se A ⊂ B, P(A)≤ P(B)
REGRA DA SOMA
Se A e B são eventos quaisquer de Ω, então: P(A ∪ B) = P(A) + P(B) – P(A ∩ B).




