Prismas: Paralelepípedos e cubos

Paralelepípedos e cubos são sólidos geométricos tridimensionais com faces retangulares. Essas figuras são fundamentais na geometria espacial, amplamente aplicadas em cálculos de volume, área e em design e engenharia, devido à sua simplicidade e propriedades bem definidas.

PARALELEPÍPEDO

É o prisma cuja base é um paralelogramo.

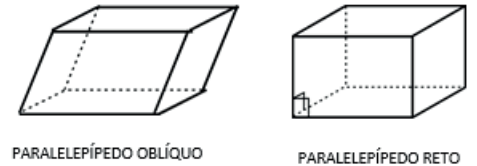
PARALELEPÍPEDO RETO RETÂNGULO

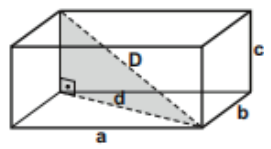
DIAGONAL DO PARALELEPÍPEDO

Do Pitágoras no triângulo retângulo de catetos a e b e hipotenusa d teremos:

d² = a² + b²

Do Pitágoras no triângulo retângulo hachurado, de catetos d e c e hipotenusa D teremos:

ÁREA TOTAL DO PARALELEPÍPEDO

Utilizaremos as áreas dos 6 retângulos, retângulos a × b, a × c e b × c.

S_T= 2ab + 2ac + 2bc = 2(ab + ac + bc)

VOLUME DO PARALELEPÍPEDO

V = S_b · H = abc

CUBO (HEXAEDRO REGULAR)

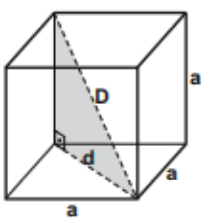
Para encontrar os elementos do cubo basta utilizarmos as mesmas definições do paralelepípedo reto-retângulo fazendo a = b =c.

DIAGONAL DO CUBO

ÁREA LATERAL DO CUBO

Teremos as áreas dos 4 quadrados laterais.

S_l = 4a²

ÁREA TOTAL DO CUBO

Áreas de todas as faces, ou seja, dos 6 quadrados.

S_T = 6a²

VOLUME DO CUBO

V = S_b · H = a³

RELAÇÕES MÉTRICAS NO HEXAEDRO REGULAR DE ARESTA A

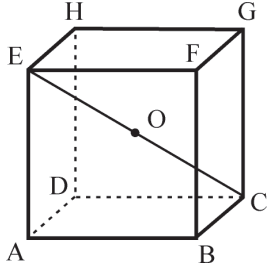
Centro do cubo: Ponto O, interseção das quatro diagonais do poliedro. O ponto O equidista dos vértices, equidista das arestas e equidista das faces do cubo.