PRISMAS
Dados um polígono ABC…MN situado num plano αα e outro polígono A’B’C’…M’N’ congruente ao primeiro e situado num plano paralelo β (β ≠ α), chama-se prisma o sólido formado pela reunião de todos os segmentos de reta com uma extremidade num ponto de ABC…MN ou em sua região interna e outra num ponto de A’B’C’...M’N’ ou em sua região interna.
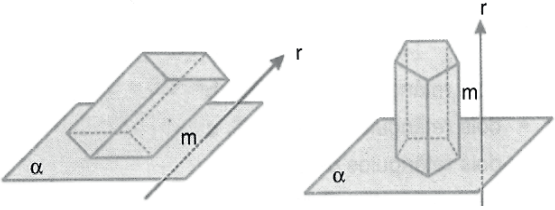
Exemplo: Prisma hexagonal
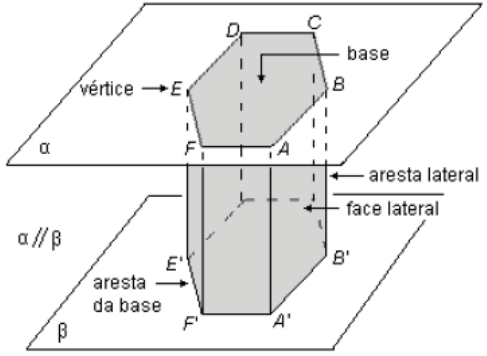
ELEMENTOS PRINCIPAIS
- Bases – formada por polígonos
- Arestas das bases – lados das bases
- Faces laterais – formadas por paralelogramos
- Altura – distância H entre os planos das bases
- Superfície lateral – conjunto de todas as faces laterais
- Superfície total – união da superfície lateral com as duas bases
CLASSIFICAÇÃO
Podemos classificar um prisma de acordo com o número de lados das duas bases.
- Prisma triangular: bases: triângulos
- Prisma quadrangular: bases: quadriláteros
- Prisma pentagonal: bases: pentágonos
- Prisma hexagonal: bases: hexágonos
Se as bases são polígonos regulares, o prisma é chamado regular.
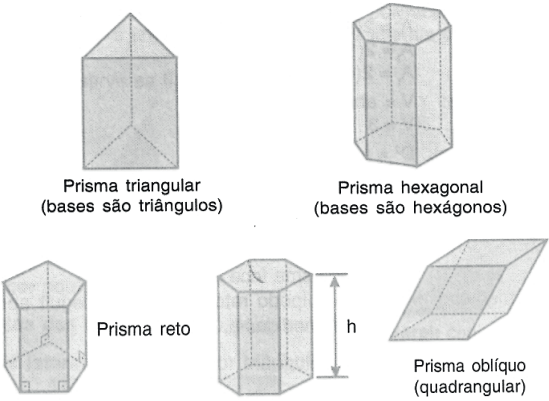
Um prisma é reto se as arestas laterais forem perpendiculares às bases; caso contrário, o prisma é dito oblíquo.
- Se as arestas laterais são perpendiculares aos planos das bases, o prisma e reto. Exemplo:
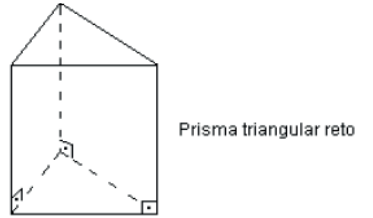
- Se as arestas laterais são obliquas aos planos das bases, o prisma e dito oblíquo.
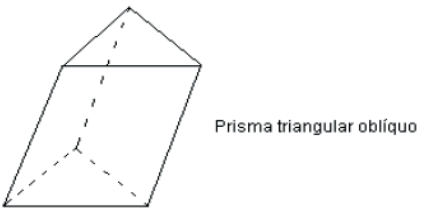
- O prisma será regular se for reto e sua base for um polígono regular.
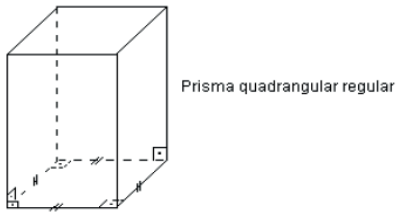
Altura do prisma e a distância entre os planos das bases.
- Área da base (SB)
É a área de uma das bases do prisma.
- Área lateral (SL)
É soma das áreas das faces laterais.
- Área total (ST)
É a soma das áreas de todas as faces do prisma.
ST = SL + 2SB
- Volume (V)
O volume do prisma é dado pelo produto da área da base pela altura:
V = SB . H




