PRISMAS
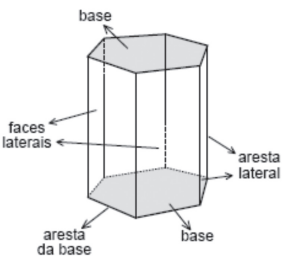
As arestas das bases são duas a duas congruentes e as arestas laterais são todas congruentes entre si.
A altura do prisma é a distância entre os planos das duas bases.
Seção de um prisma é a interseção do prisma com um plano que intercepte todas as arestas laterais.
A seção reta ou seção normal é a seção cujo plano é perpendicular às arestas laterais.
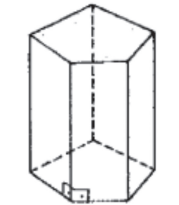
Prisma reto: possui arestas laterais perpendiculares aos planos das bases e as faces laterais são retângulos.
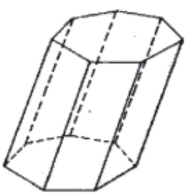
Prisma oblíquo: as arestas laterais são oblíquas aos planos das bases.
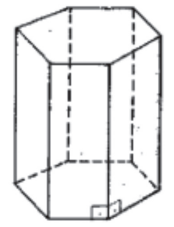
Prisma regular: prisma reto cujas bases são polígonos regulares.
Natureza de um prisma: o prisma será triangular, quadrangular, pentagonal, etc, conforme a base seja um triângulo, quadrilátero, pentágono, etc.
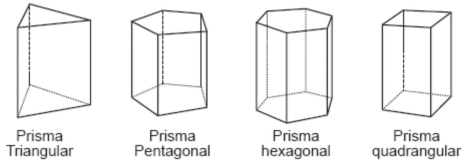
Paralelepípedo: prisma cujas bases são paralelogramos.
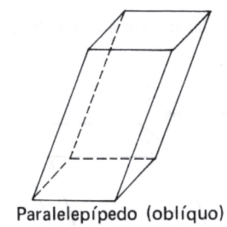
Paralelepípedo reto: prisma reto cujas bases são paralelogramos.
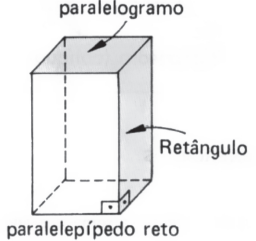
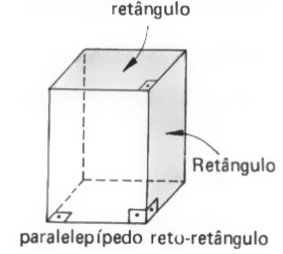
Paralelepípedo reto-retângulo ou paralelepípedo retângulo ou ortoedro: prisma reto cujas bases são retângulos.
Hexaedro regular ou cubo: paralelepípedo retângulo cujas arestas são todas congruentes.
PARALELEPÍPEDO RETÂNGULO
Seja um paralelepípedo retângulo de dimensões a, b e c, temos:
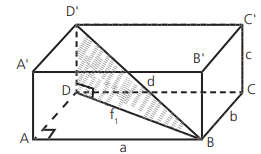
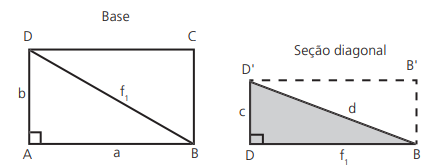
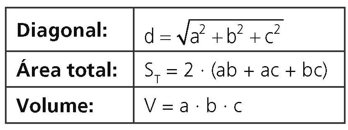
No caso particular do cubo de aresta a, a diagonal é d = a√3, a área total é ST = 6a2 e o volume é V = a3.
ÁREA LATERAL, ÁREA TOTAL E VOLUME DO PRISMA
Área lateral (SL ): área de todas as faces laterais.
Área total (ST ): área lateral mais a área das bases.
Seja um prisma onde:
a → aresta lateral
2p → perímetro da seção reta
h → altura
SB → área da base
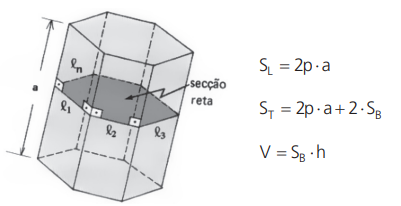
No prisma reto, a aresta lateral é igual a altura (a=h) e a seção reta é a própria base.
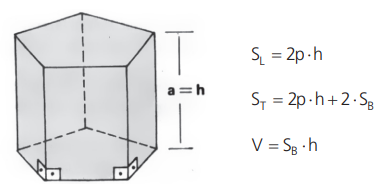
PRINCIPAIS PRISMAS
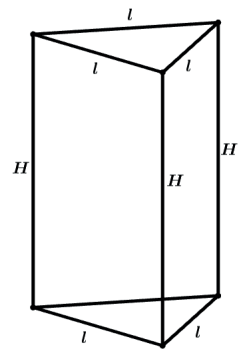
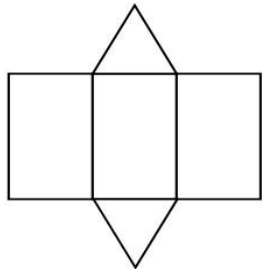
Em qualquer prisma reto as faces laterais serão retângulos e dessa forma a área lateral será dada por todos esses retângulos. Chamando a aresta da base de l e sendo a altura do prisma H teremos que a área de cada retângulo da face lateral será l. H.
PRISMA TRIANGULAR REGULAR

PRISMA QUADRANGULAR REGULAR
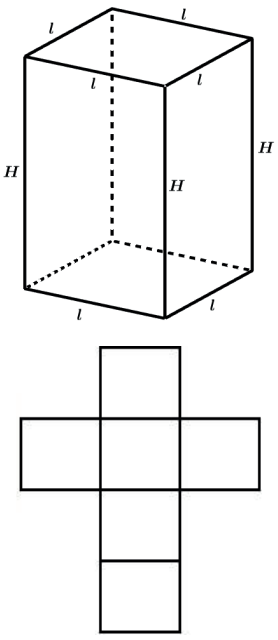
Área da base: SB = I2
Área lateral: SI = 4 · I · H
Área total: ST = 4|H + 2|2
Volume: V = I2 ⋅ H
PRISMA HEXAGONAL REGULAR
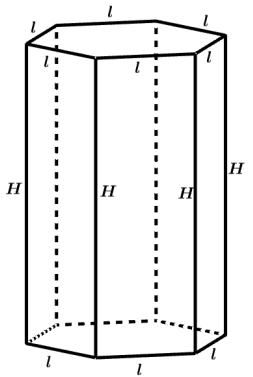
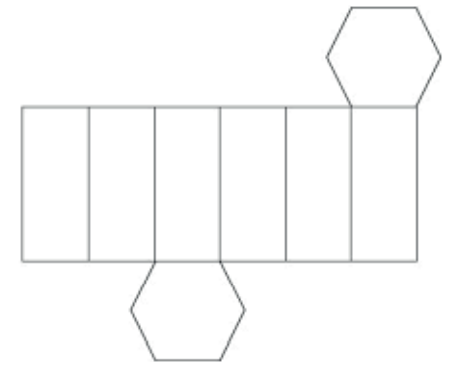
Área da base: SB = I2
Área lateral: SI = 4 · I ⋅ H
Área total: ST = 4|H + 2|2
Volume: I2 . H




