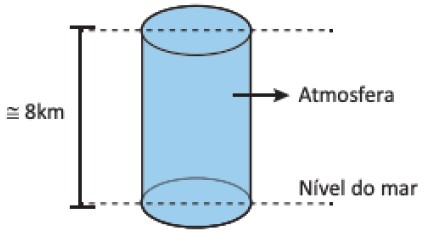
PRESSÃO ATMOSFÉRICA
A atmosfera exerce uma pressão em todos nós. No nível do mar, essa camada de ar é de aproximadamente 8000 m. Uma cidade a 1000 m de altitude está sob uma camada menor de ar, ou seja, a pressão atmosférica é menor. Vamos calcular a pressão atmosférica no nível do mar.

Em que a força é o peso de uma coluna de ar que é exercida em uma área (A). Logo:

Sendo µ a massa específica do ar/líquido e h a altura (profundidade) da coluna de arlíquido que está sobre um ponto, exercendo uma pressão p sobre este.
Unidade: Além de N/m², podemos usar Pa (Pascal). Também é unidade do S.I. Outra unidade (usual) é atm.
Sabendo-se que a massa específica de ar vale aproximadamente 1,25 kg/m³ (a temperatura do ar próximo à superfície é diferente da temperatura do ar a 5000 m de altitude, o que afeta na densidade de ar, mas vamos considerar que, na média, a densidade será 1,25 kg/m³ e constante), temos que:
P = μgh ≅ 1,25 · 10 · 8000 ∴ P = 105 Pa = 1 atm
PRESSÃO EM LÍQUIDOS INCOMPRESSÍVEIS EM REPOUSO
A densidade de um líquido muda muito pouco quando é submetido a diferentes pressões. Por exemplo, a densidade da água varia 0,5% quando a pressão varia de 1 atm a 100 atm, à temperatura ambiente. Podemos dizer, então, que os líquidos são incompressíveis, ou seja, têm densidade constante.
Antes de deduzirmos a lei de Stevin, precisamos entender como calcular a pressão que uma coluna líquida exerce sobre uma superfície. Sendo assim, consideremos a situação da figura abaixo, em que um tubo, cuja área da base é A, contém um líquido de densidade d, até uma altura h. Vamos calcular a pressão exercida por essa coluna liquida sobre a base do tubo.
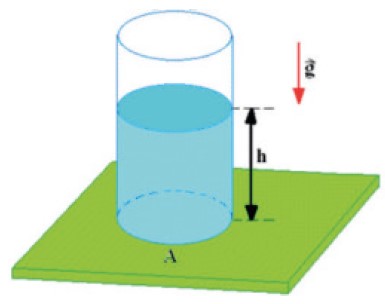
Volume do líquido: V = Abase · h
Massa do líquido: μm = μ · V
Logo, por definição da pressão é calculada como:

Utilizando o raciocínio anterior, podemos calcular a pressão que um líquido exerce a uma profundidade h, como:
P = Patm + μgh
Em que Patm é a pressão atmosférica local.
Podemos ver que a pressão aumenta com a profundidade, ou seja, ponto na mesma horizontal sofrem a mesma pressão.
VASOS COMUNICANTES
A lei de Stevin nos fornece a diferença de pressão entre dois pontos quaisquer de um líquido em equilíbrio, independentemente da forma do recipiente.
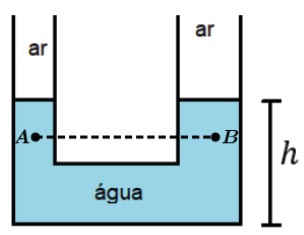
Estando os pontos A e B no mesmo nível teremos
Px = Py
Desse modo, estando os dois lados do recipiente submetidos à mesma pressão nos dois lados, pressão atmosférica por exemplo, o nível do líquido deve ser o mesmo nos dois lados
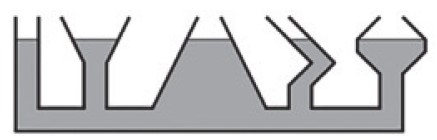
Se colocarmos em vasos comunicantes líquidos diferentes e imiscíveis, na posição de equilíbrio poderemos ter desníveis entre as superfícies livres.
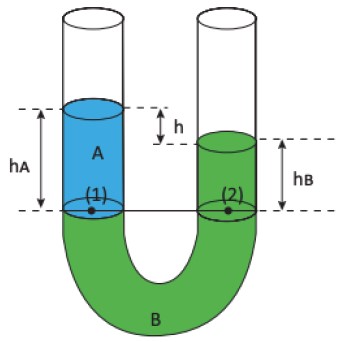
Como a pressão em pontos de mesmo nível é a mesma, podemos afirmar que a pressão no ponto 1 é igual a do 2, ou seja

Observação: Se um dos lados estiver tampado (sem ar), não haverá pressão atmosférica. Vamos supor que, na situação anterior, o lado B estivesse tampado. Teríamos que:





