POTÊNCIAS DE i
Temos:

Observe que as quatro potências de i na coluna da esquerda, repetem-se nos quatro casos seguintes na coluna da direita. Este ciclo 1, i,-1,-i repete-se indefinidamente. Então, para simplificar ix para x>4, buscamos o maior múltiplo de 4 contido em x; por exemplo

REPRESENTAÇÃO DOS NÚMEROS COMPLEXOS
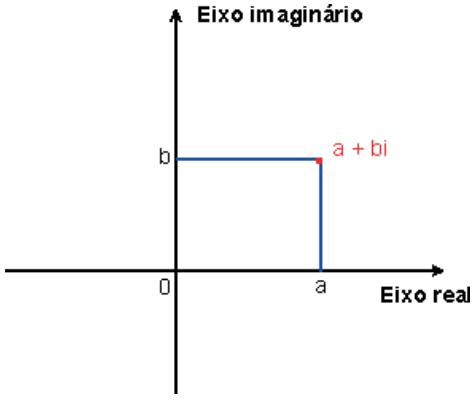
Um número complexo é constituído por duas componentes: a parte real e a parte imaginária. Isso sugere a utilização de dois eixos para representá-lo: um para a parte real e o outro para a parte imaginária. Esses dois eixos chamam-se eixo real e eixo imaginário, respectivamente. O plano determinado por esses dois eixos chama-se plano complexo ou plano de Argand-Gauss.
Para desenharmos o gráfico do número complexo a+bi, marcamos o ponto (a ; b) no plano.
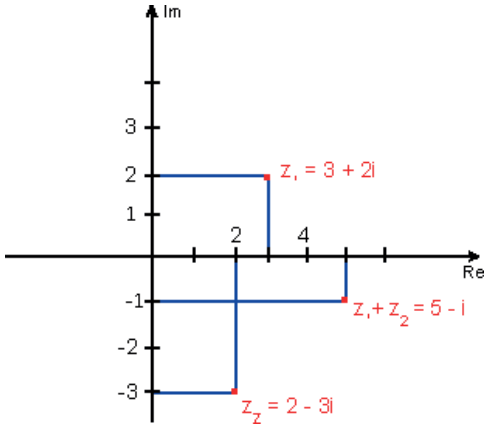
Exemplo:
MÓDULO DE NÚMERO COMPLEXO
O módulo (ou valor absoluto) do número complexo a + bi é distância de a + bi à origem do plano complexo.
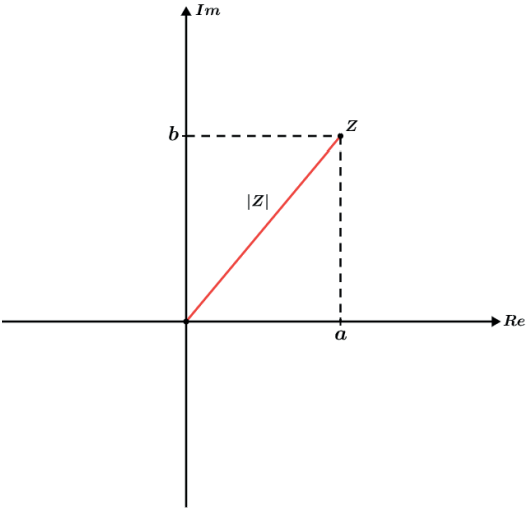
Usando o Teorema de Pitágoras, concluímos que a distância de (a : b) a(0 : 0) é

DEFINIÇÃO
O módulo (ou valor absoluto) do complexo:





