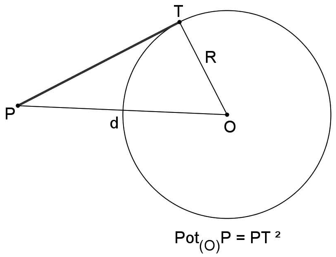
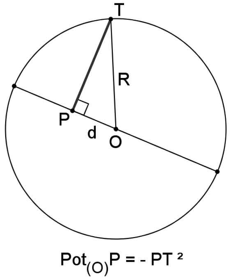
A potência de um ponto P em relação a um círculo de centro O e raio R é dada por Pot(O)P = d2 − R2, onde d é a distância de P ao centro do círculo.
P exterior ao círculo ⇒ d > R ⇒ Pot(O)P > 0
P pertence ao círculo ⇒ d = R ⇒ Pot(O)P = 0
P interior ao círculo ⇒ d < R ⇒ Pot(O)P < 0
Se um ponto está sobre uma circunferência, então a sua potência em relação à essa circunferência é nula.
Observe nas figuras a seguir que, pelo teorema de Pitágoras, temos PT2 = |d2 − R2| = |Pot(O)P|.
Exemplo:
Considerando o círculo da figura de centro O, calcule Pot(O)A + Pot(O)B + Pot(O)C.
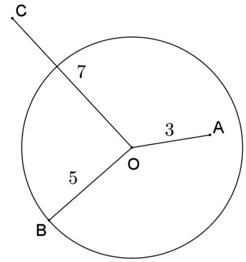
Resolução:

POTÊNCIA DE PONTO EXTERIOR
Se por um ponto P exterior a uma circunferência são traçadas duas secantes PAB e PCD a essa circunferência, então PA ⋅ PB = PC ⋅ PD.
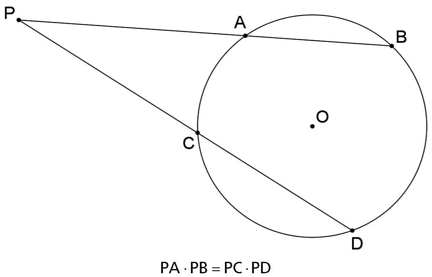
Exemplo:
Calcule x na figura a seguir:
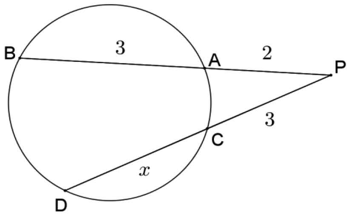
Resolução:

Se por um ponto P exterior a uma circunferência são traçadas uma secante PAB e uma tangente PT a essa circunferência, então PT2 = PA ⋅ PB.
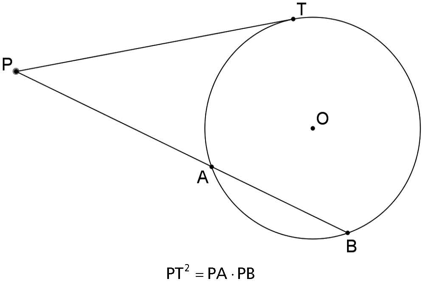
Exemplo:
Calcule x na figura a seguir:
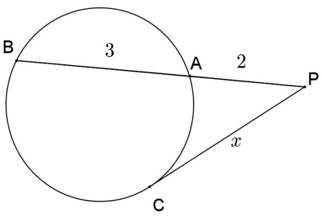
Resolução:
Sabe-se que PC2 = PA ⋅ PB ⇔ x2 = 2 ⋅ 5 ⇔ x = √10.
Se por um ponto P exterior a uma circunferência de raio R e distante d unidades de seu centro (d > R) é traçada uma secante PAB a essa circunferência, então PA ⋅ PB = d2 − R2.
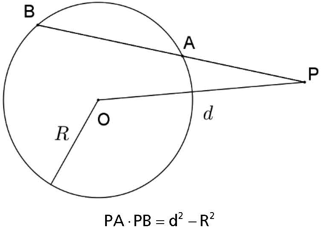
Exemplo:
Seja P um ponto exterior a um círculo de centro O e raio P e tal que OP = R√3. Traça-se por P a secante PAB ao círculo. Se PA = R, então calcule AB em função de R.
Resolução:
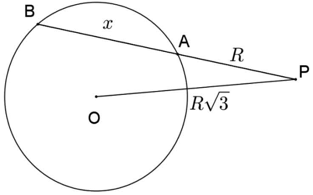
Usando a proposição anterior, temos:

Observe que você poderia prolongar PO até encontrar a circunferência, obtendo uma segunda secante, e encontraria a mesma relação.
POTÊNCIA DE PONTO INTERIOR
Se por um ponto P interior a uma circunferência são traçadas duas cordas APB e CPD nessa circunferência, então PA⋅PB=PC⋅PD.
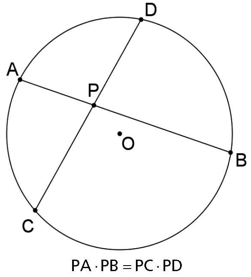
Exemplo:
Calcule x na figura a seguir:
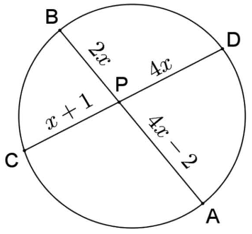
Resolução:
AP ⋅ BP = CP ⋅ DP
(4x−2) ⋅ 2x = (x + 1) ⋅ 4x
4x2 − 8x = 0
4x(x − 2) = 0
x = 2
Note que como 2x e 4x são medidas de segmentos de reta, então x ≠ 0.
Se por um ponto P interior a uma circunferência de raio R e distante d unidades de seu centro (d < R) é traçada uma corda APB nessa circunferência, então PA ⋅ PB = R2 − d2.
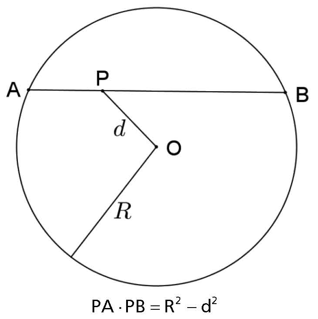
Exemplo:
Calcule x na figura, onde O é o centro da circunferência.
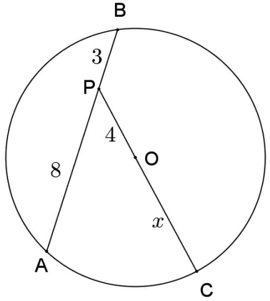
Resolução:
PA ⋅ PB = R2 − d2 ⇔ 8 ⋅ 3 = x2 − 42 ⇔ x2 = 8 ⇔ x = 2√2
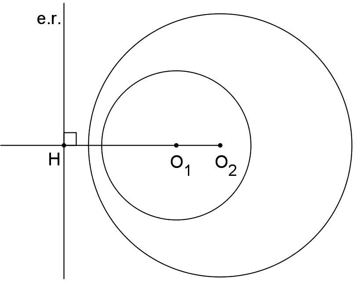
EIXO RADICAL
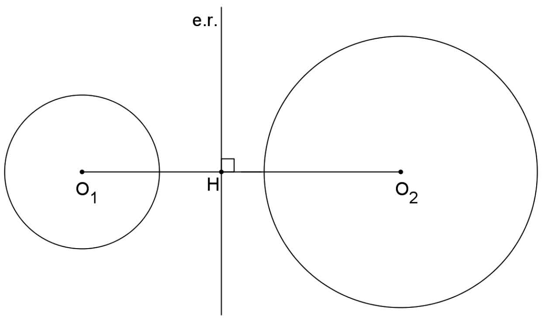
O lugar geométrico dos pontos cujas potências em relação a dois círculos não concêntricos são iguais é uma reta perpendicular à reta que une os centros dos dois círculos e é chamado eixo radical dos círculos.
Se (e.r.) é o eixo radical dos círculos de centro O1 e O2, então P ∈ (e.r.) ⇔ Pot(O1)P = Pot(O2)P.
A seguir apresentamos a posição do eixo radical para as diversas posições relativas entre os círculos.
- CIRCUNFERÊNCIAS EXTERIORES
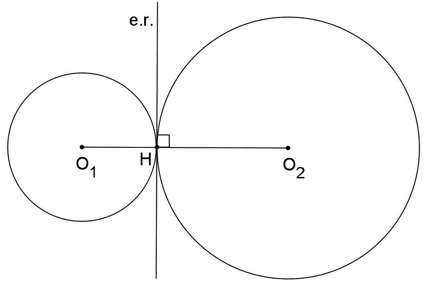
- CIRCUNFERÊNCIAS TANGENTES EXTERIORMENTE
- CIRCUNFERÊNCIAS SECANTES
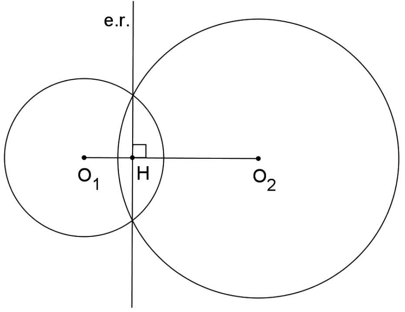
- CIRCUNFERÊNCIAS TANGENTES INTERIORMENTE
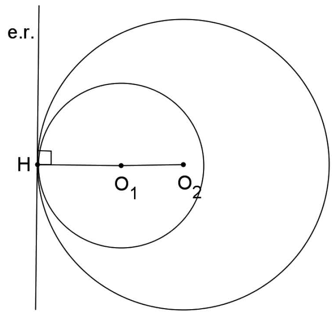
- CIRCUNFERÊNCIAS INTERIORES