Serve para efetuar a divisão de um polinômio P(x) por um binômio da forma (ax + b).
Exemplo:
Determinar o quociente e o resto da divisão do polinômio P(x) = 3x3 – 5x2 + x – 2 por (x – 2).
Resolução:
Observe que o grau de Q(x) é uma unidade inferior ao de P(x), pois o divisor é de grau 1.
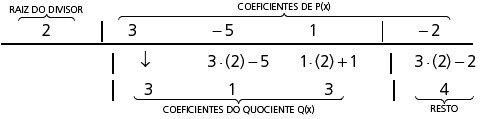
Resposta: Q(x) = 3x2 + x + 3 e R(x) = 4.
Para a resolução desse problema seguimos os seguintes passos:
1º) Colocamos a raiz do divisor e os coeficientes do dividendo ordenadamente na parte de cima da “cerquinha”.
2º) O primeiro coeficiente do dividendo é repetido abaixo.
3º) Multiplicamos a raiz do divisor por esse coeficiente repetido abaixo e somamos o produto com o 2º coeficiente do dividendo, colocando o resultado abaixo deste.
4º) Multiplicamos a raiz do divisor pelo número colocado abaixo do 2º coeficiente e somamos o produto com o 3º coeficiente, colocando o resultado abaixo deste, e assim sucessivamente.
5º) Separamos o último número formado, que é igual ao resto da divisão, e os números que ficam à esquerda deste serão os coeficientes do quociente.




