POLÍGONO REGULAR
A área de um polígono regular é igual ao produto do semiperímetro pelo apótema.
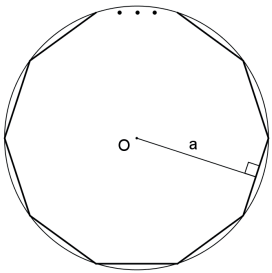
Seja um polígono regular de semiperímetro p e apótema a, então sua área é S = p ⋅ a.
Demonstração:
Seja um polígono regular de gênero n, lado x e apótema a. Ele pode ser dividido em n triângulos isósceles de vértice no centro do círculo circunscrito ao polígono, cuja base é o lado e a altura é o apótema do polígono. A área de cada um desses triângulos isósceles é SΔ = x⋅a/2. Portanto, a área do polígono é dada por S=n ⋅ SΔ = n ⋅ x⋅a/2 = nx/2 ⋅ a = p ⋅ a, onde utilizamos p = n⋅x/2.
REGIÕES CIRCULARES
CÍRCULO
A área do círculo é o produto do quadrado do seu raio pelo número irracional ππ.
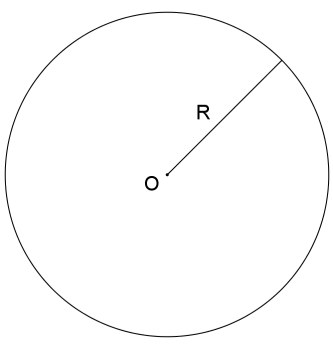
Seja um círculo de raio R, então sua área é S = π ⋅ R2.
Demonstração:
Observe que a área do círculo pode ser calculada considerando-o um polígono regular cujo número de lado tende ao infinito. Assim, sua área é p produto do seu semiperímetro 2πR/2 = πR pelo seu apótema R, ou seja, S = πR ⋅ R = π ⋅ R2.
SETOR CIRCULAR
Um setor circular é a região da circunferência delimitada por dois raios e um arco e é caracterizado pelo ângulo central por ele determinado.
A área do setor circular é igual à metade do produto do quadrado do raio pelo ângulo central em radianos.
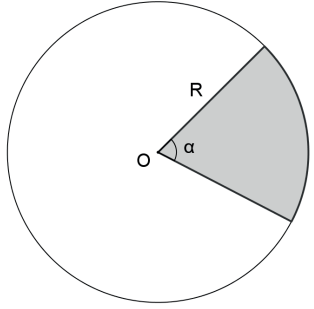
Seja um setor circular de ângulo central α em radianos e de raio R, então sua área é:

Observe que se o ângulo central estiver expresso em graus, a expressão resultante é:

Demonstração:
A área do setor circular é proporcional ao ângulo central. Assim, um setor circular de α radianos representa α/2π da área total do círculo, ou seja:

SEGMENTO CIRCULAR
Um segmento circular é uma região da circunferência delimitada por uma corda e um arco e também é caracterizado pelo ângulo central associado à corda.
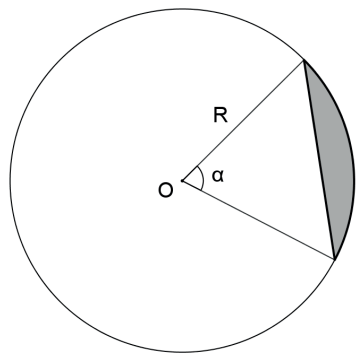
Seja um segmento circular de α em radianos e de raio R, então sua área é:





