DIMENSÕES LINEARES DA PIRÂMIDE
Na figura a seguir, temos uma pirâmide regular, na qual vamos destacar alguns segmentos importantes. A medida de cada um estará sendo representada por uma letra.
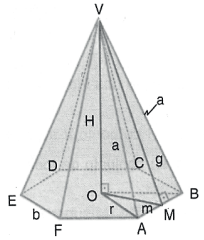
- Aresta da base (b)
- Apótema da base (m)
- Raio da base (r)
- Altura (h)
- Aresta lateral (a)
- Apótema da pirâmide (g) ou (M)
Chama-se apótema de uma pirâmide regular cada uma das alturas de suas faces laterais, relativas às arestas da base.
Os triângulos VOM, VOB e VMB são retângulos. Aplicando-se o teorema de Pitágoras, obtemos algumas relações importantes entre as dimensões lineares citadas anteriormente. Vejamos:
- No triângulo VOM: g² = H² + m²
- No triângulo VOB: a² = H² + r²
- No triângulo VMB: a² = g² + (b/2)²
ÁREAS
Superfície Lateral é a reunião das faces laterais. Já a Superfície Total é a reunião das faces laterais com a base.
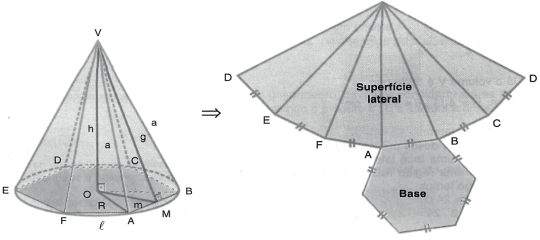
Indicando por SB, SL e ST, respectivamente, as áreas da base, da superfície lateral e da superfície total de uma pirâmide, temos:
ST = SB + SL
SB = (dependerá do polígono da base)
SL = soma das áreas das faces laterais
Lembrando que as principais bases serão a triangular, que teremos SB = ℓ²√3/4, a base quadrada onde SB = ℓ2 e a base hexagonal que é formada por 6 triângulos equiláteros, assim SB = 6 ⋅ ℓ²√3/4 = 3ℓ²√3/2.
VOLUME
O volume de uma pirâmide é a terça parte do volume de um prisma de base e altura iguais às da pirâmide. Assim temos
V = SB.H/3
TETRAEDRO REGULAR
Chama-se tetraedro regular o tetraedro que possui as seis arestas congruentes entre si. Nesse caso, todas as faces são triângulos equiláteros. O tetraedro é uma pirâmide triangular.
Para o cálculo da área total, da altura e do volume de um tetraedro regular, utilizamos:
ST = a²√3
H = a√6/3
V = a³√2/12
RELAÇÕES MÉTRICAS NO OCTAEDRO REGULAR DE ARESTA A
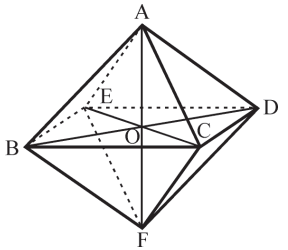
BCDE, ABFD e ACFE são quadrados de lado a.
Diagonal do octaedro: AF = BD = CE = a√2.
Centro do octaedro: Ponto O, interseção das três diagonais. O ponto O equidista dos vértices, equidista das faces e equidista das arestas do octaedro.




