PIRÂMIDE
A pirâmide é um sólido delimitado por faces planas. Sua base é um polígono e suas faces laterais são triângulos. Observe as figuras seguintes:
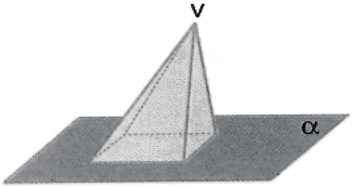
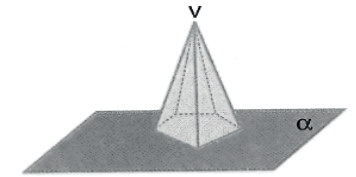
ELEMENTOS PRINCIPAIS
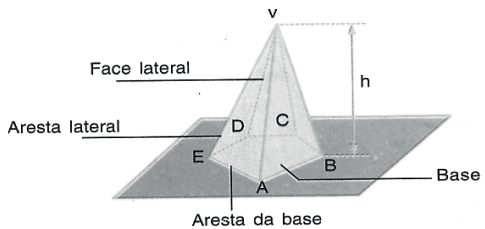
Base: formada por polígono
Vértice: ponto V
Arestas da Base: lados do polígono da base
Faces laterais: formada por triângulos
Arestas laterais: lados dos triângulos das faces laterais, com exceção dos lados do polígono da base Altura: distância H do ponto V ao plano da base
Superfície lateral: conjunto de todas as faces
Superfície total: união da superfície lateral com a base
CLASSIFICAÇÃO
Podemos classificar uma pirâmide de acordo com o tipo de polígono que constitui a sua base.
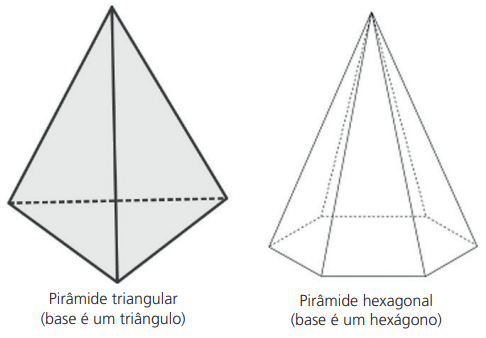
Pirâmide triangular – base é um triângulo
Pirâmide quadrangular – base é um quadrilátero
Pirâmide pentagonal – base é um pentágono}
Pirâmide hexagonal – base é um hexágono
Se a base é um polígono regular, a pirâmide é chamada regular. As arestas laterais são congruentes entre si e as faces laterais são triângulos isósceles congruentes entre si.
DIMENSÕES LINEARES DA PIRÂMIDE
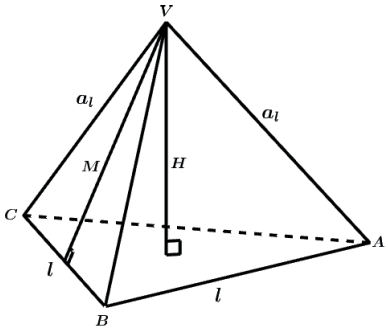
Na figura a seguir, temos uma pirâmide regular, na qual vamos destacar alguns segmentos importantes. A medida de cada um estará sendo representada por uma letra.
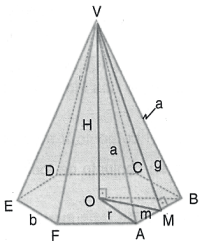
Aresta da base (b)
Apótema da base (m)
Raio da base (r)
Altura (h)
Aresta lateral (a)
Apótema da pirâmide (g) ou (M)
Chama-se apótema de uma pirâmide regular cada uma das alturas de suas faces laterais, relativas às arestas da base.
Os triângulos VOM, VOB e VMB são retângulos. Aplicando-se o teorema de Pitágoras, obtemos algumas relações importantes entre as dimensões lineares citadas anteriormente. Vejamos:
No triângulo VOM: g2 = H2 + m2
No triângulo VOB: a2 = H2 + r2
No triângulo VMB: a2 = g2 + ( b/2 )2
Veremos mais adiante de forma mais detalhada.
ÁREAS
Superfície Lateral é a reunião das faces laterais. Já a Superfície Total é a reunião das faces laterais com a base.
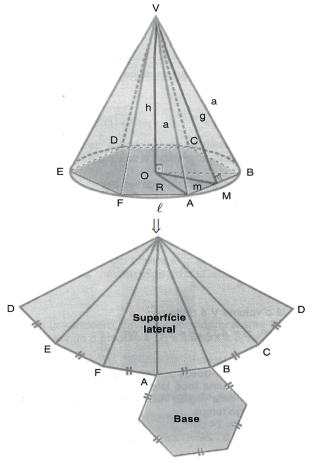
Indicando por SB, SL e ST, respectivamente, as áreas da base, da superfície lateral e da superfície total de uma pirâmide, temos:
ST = SB + SL
SB = (dependerá do polígono da base)
SL = soma das áreas das faces laterais
Lembrando que as principais bases serão a triangular, que teremos SB = I2√3/4 , a base quadrada onde SB = I2 e a base hexagonal que é formada por 6 triângulos equiláteros, assim:

VOLUME
O volume de uma pirâmide é a terça parte do volume de um prisma de base e altura iguais às da pirâmide. Assim temos:

ENCONTRANDO A ALTURA DE UMA PIRÂMIDE
Basicamente podemos aplicar dois Pitágoras diferentes quando queremos obter relações entre a altura de uma pirâmide e os seus outros elementos.
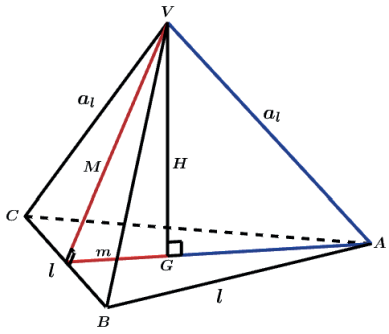
A projeção da altura sempre se dará sobre o centro de gravidade do polígono da base (baricentro). Podemos ter dois triângulos retângulos possíveis para aplicar o teorema de Pitágoras.
TRIÂNGULO 1
Nesse primeiro triângulo teremos o triângulo formado pela altura H, pela distância do centro do polígono ao lado, que é o apótema da base (m) e a hipotenusa que é o apótema da pirâmide (M). O apótema da base é diferente para cada polígono regular que temos na base.
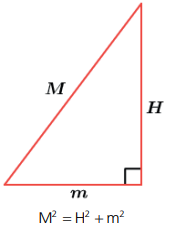
TRIÂNGULO 2
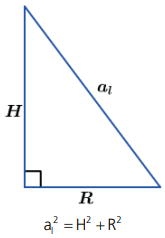
Nesse segundo triângulo teremos o triângulo formado pela altura H, pela distância do centro do polígono ao vértice, que é o raio da circunferência circunscrita ao polígono da base, que chamaremos aqui de R e a hipotenusa que é a aresta lateral (al). O raio da circunferência circunscrita ao polígono da base da base é diferente para cada polígono regular que temos na base.
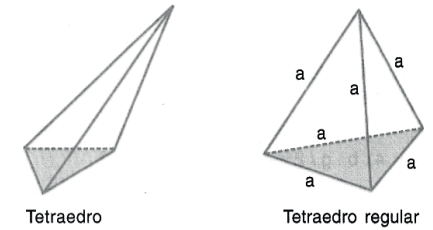
TETRAEDRO REGULAR
Chama-se tetraedro regular o tetraedro que possui as seis arestas congruentes entre si. Nesse caso, todas as faces são triângulos equiláteros. O tetraedro é uma pirâmide triangular.
Vamos utilizar um dos possíveis Pitágoras aplicados a pirâmide para chegarmos a altura H em função da aresta a do tetraedro regular. Vamos utilizar a propriedade do baricentro do triângulo retângulo que divide a altura na razão de 2:1. Fica para você chegar no valor da altura H e consequentemente no volume V. Para o cálculo da área total, da altura e do volume de um tetraedro regular, utilizamos:

PRINCIPAIS PIRÂMIDES
PIRÂMIDE TRIANGULAR REGULAR

PIRÂMIDE QUADRANGULAR REGULAR
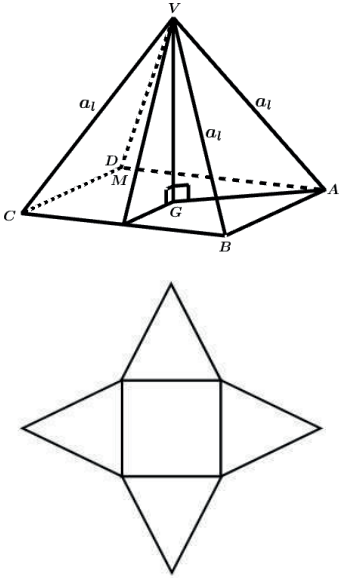

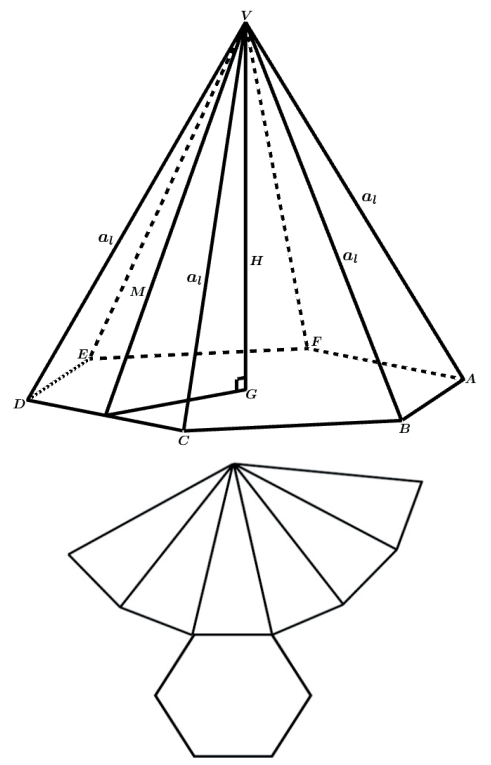
PIRÂMIDE HEXAGONAL REGULAR

RELAÇÕES MÉTRICAS NO OCTAEDRO REGULAR DE ARESTA a
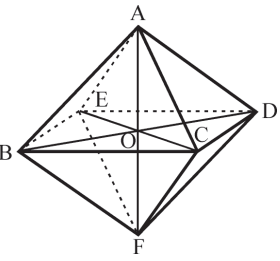
BCDE, ABFD e ACFE são quadrados de lado a.

Centro do octaedro: Ponto O, interseção das três diagonais. O ponto O equidista dos vértices, equidista das faces e equidista das arestas do octaedro.




