PARÁBOLA
Definição geométrica: é a cônica obtida mediante a secção de um plano secante a um cone quadrático, sendo o plano paralelo a uma e somente uma geratriz do cone.
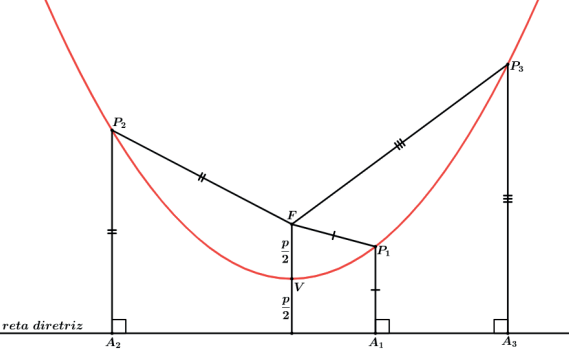

ELEMENTOS DA PARÁBOLA
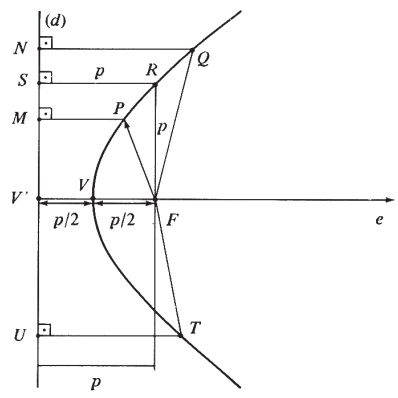
- Pontos principais:
F – foco
V – vértice
- Segmentos:
V’F=p – parâmetro (semicorda focal mínima)
FP→ – raio vetor
- Relação:
VF = p/2
- Reta e eixo: a reta fixa (d) é a diretriz e e, eixo que passa pelo foco e é perpendicular à diretriz, eixo de simetria da parábola.
EQUAÇÃO DA PARÁBOLA
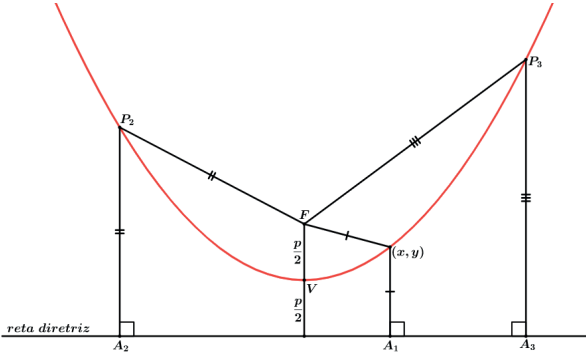
Fazendo o ponto genérico (x, y) e utilizando um sistema cartesiano adequado de forma que o vértice esteja centrado na origem (0, 0) o foco F será F(0, p/2). Vamos aplicar distância entre 2 pontos.

A reta diretriz tem equação y =− p/2, vamos aplicar distância do ponto (x,y) a reta diretriz e igualar a mesma distância d.

Igualando as distâncias

Dessa forma nossas equações de parábolas com vértice na origem serão
- Parábola com reta diretriz paralela a Ox↔
x2 = 2 py
- Parábola com reta diretriz paralela a Oy↔
y2 = 2 px
Fazendo a translação de eixos adequada teremos
- Parábola com reta diretriz paralela a Ox↔
(x − x0)2 = 2p(y − y0)
- Parábola com reta diretriz paralela a Oy↔
(y − y0)2 = 2p(x − x0)
Vamos encontrar os elementos da parábola.
- Reta diretriz paralela a Ox↔
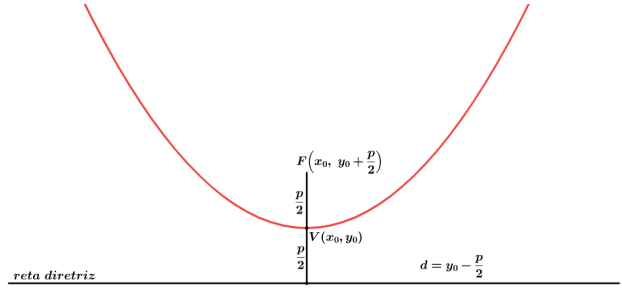
*Concavidade para baixo

- Reta diretriz paralela a Oy↔
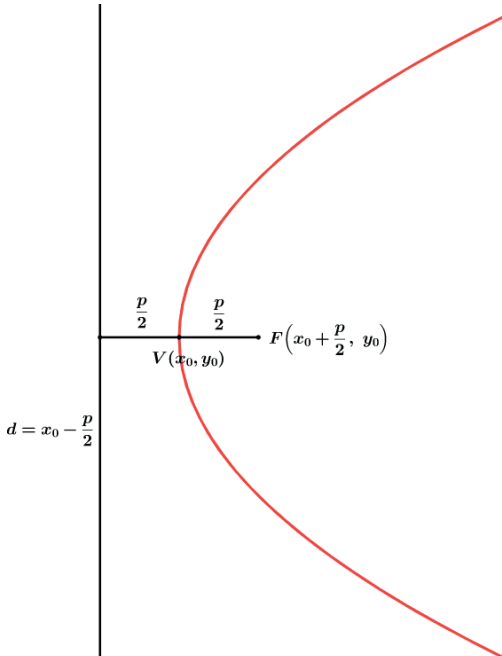
*Concavidade para esquerda

Por exemplo a parábola de equação (x + 1) = (y − 3)2, teremos o número 1 multiplicando (y − 3)2 daí 2p =1 ⇒ p = 1/2 ⇒ p/2 = 1/4 . Teremos uma parábola com reta diretriz paralela ao eixo Oy↔.

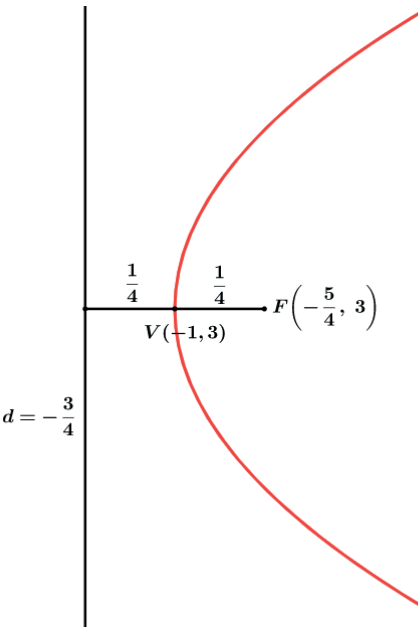
EQUAÇÃO COMPLETA
Vamos expandir a equação do exemplo anterior.
(x + 1) = (y − 3)2 ⇒ x + 1 = y2 − 6y + 9 ⇒ x = y2 − 6y + 8
Dessa forma final x = y2 − 6x + 8 não sabemos as coordenadas do vértice ou do foco ou o valor do parâmetro p, apenas sabemos que se trata de uma parábola de reta diretriz paralela a Oy↔ (o y está ao quadrado) e possui concavidade para direita (o coeficiente de y2 é positivo). Vamos usar a mesma técnica usada em todas as equações de cônicas, completar quadrados.
x = y2 − 6y + 8 + 1 − 1 ⇒ x + 1 = y2 − 6y + 9 ⇒ (x + 1) = (y − 3)2
O que para a equação da parábola se torna bem mais imediato, a partir daí identificamos os valores necessários.




