Parábola

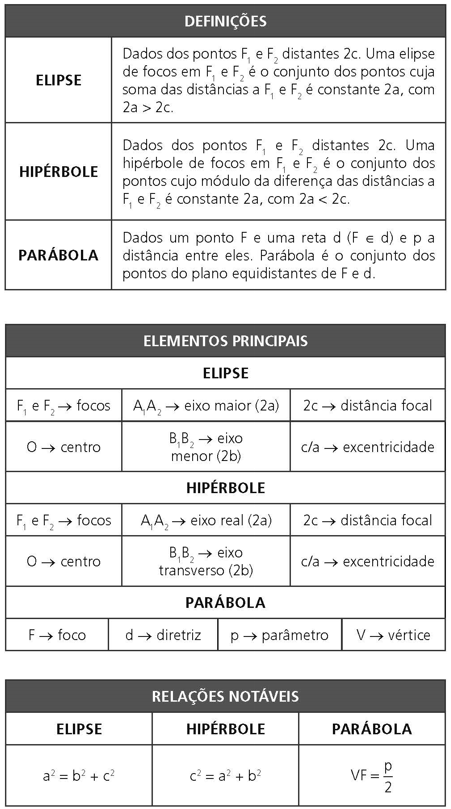
ELEMENTOS DA PARÁBOLA

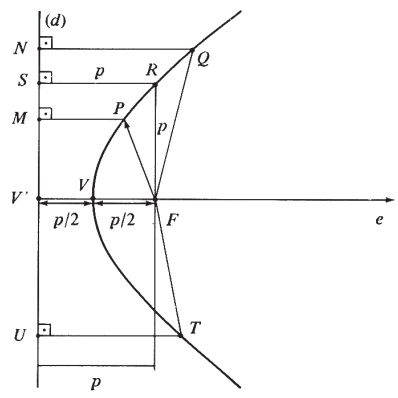
• Pontos principais:

F – foco
V – vértice

• Segmentos:

V’F=p – parâmetro (semicorda focal mínima)
FP→ – raio vetor

• Relação:

VF = ^p/₂

• Reta e eixo: a reta fixa (d) é a diretriz e e, eixo que passa pelo foco e é perpendicular à diretriz, eixo de simetria da parábola.

EQUAÇÕES

Equação espontânea. No sistema foco-diretriz a equação espontânea da parábola é:

De acordo com a definição, temos:

FP = |MP∣ ⇔ u = v    (1)

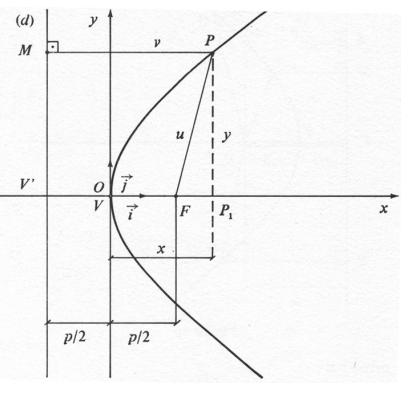
• Equação reduzida: o ponto F tem coordenadas (^p/₂ , 0)

Calculemos u e v:

Igualando, conforme (1), vem:

Discutamos essa equação:

i. Interseções

Para x = 0, y = 0. A curva representativa de (2) passa pela origem.

II. Simetria

Trata-se de uma curva simétrica apenas em relação ao eixo x.

III. Extensão

Resolvendo a equação (2) em relação a y, vem:

Onde se conclui: se p > 0, não há valores reais de y para x < 0; se p < 0, não há valores reais de y para x > 0. A valores acrescentes de x, em valor absoluto, correspondem valores crescentes de y. Se x tende para ∞, y tende para ∞. A curva é aberta, estendendo-se indefinidamente no plano dos eixos coordenados, à direita do eixo y para p > 0 e à esquerda desse eixo para p < 0.

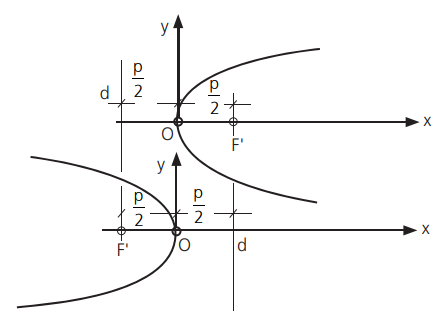
ProBizu:

Imagem geométrica

Conclui-se por essa discussão que a cônica de equação (2) é uma parábola de eixo horizontal coincidente com o eixo x e vértice na origem, tendo a concavidade voltada para a direita se p > 0 e para a esquerda se p < 0.

• Se V=0 e o eixo de simetria coincidir com o eixo dos y.

As coordenadas do foco passam a ser (0, ^p/₂) , então a equação da parábola toma a forma

x² = 2py

e a da diretriz

• Quando a parábola tem V(m, n), portanto, V ≠ 0 e o eixo de simetria paralelo ao eixo 0x, vem:

(y’)² = 2px’

e aplicando a translação de eixos de I resulta:

(y − n)² = 2p(x − m) ou (y − n)² = −2p(x − m)

• Equação geral: a equação geral é obtida, como vimos, desenvolvendo as reduzidas. Assim: (y − n)² = 2p(x − m), parábola com eixo horizontal:

Se ¹/_2p > 0, concavidade à direita e ¹/_2p < 0, concavidade à esquerda.

De (x − m)² = 2p(y − n), parábola com eixo vertical:

Se ¹/_2p > 0, concavidade para cima e ¹/_2p < 0, concavidade para baixo.

Uma equação do 2º grau com duas variáveis representa uma parábola com eixo horizontal ou vertical se, e somente se, for redutível às formas

x = ay² + by + c, com a ≠ 0   (3)

ou

y = ax² + bx + c, com a ≠ 0   (4)

Comparando (1) e (3):

De modo análogo, comparando (2) e (4), concluímos que o vértice é:

CÔNICAS – RESUMO TEÓRICO