Operações com polinômios: soma, subtração, produto e divisão

SOMA E SUBTRAÇÃO DE POLINÔMIOS

Da álgebra elementar, temos que só podemos somar e/ou subtrair termos semelhantes, ou seja, termos que possuam expoentes iguais.

Exemplo:
P(x) = 3x⁴ – 7x³ + 5x² + 12x – 8 e Q(x) = x⁴ – 12x² + 7x + 2
P(x) + Q(x) = 4x⁴ – 7x³ – 7x² + 19x – 6
P(x) – Q(x) = 2x⁴ – 7x³ + 17x² + 5x – 10

PRODUTO DE POLINÔMIOS

O produto de polinômios também segue da álgebra elementar se dando pela distributiva.

Exemplo:
Sejam P(x) = x³ – 1 e H(x) = x² – x + 1. Calcular P(x) · H(x).
P(x) · H(x) = (x³ -1) (x² – x + 1) = x⁵ – x⁴ + x³ – x² + x – 1

DIVISÃO DE POLINÔMIOS

Sejam dois polinômios P(x) e D(x), com D(x) não nulo.

Efetuar a divisão de P por D é determinar dois polinômios Q(x) e R(x), que satisfaçam as duas condições abaixo:

1ª) Q(x) · D(x) + R(x) = P(x)
2ª) gr(R) < gr(D) ou R(x) = 0

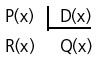
Nessa divisão:
P(x) é o dividendo.
D(x) é o divisor.
Q(x) é o quociente.
R(x) é o resto da divisão.

Observação: Quando temos R(x)=0 dizemos que a divisão é exata, ou seja, P(x) é divisível por D(x) ou D(x) é divisor de P(x).

Se D(x) é divisor de P(x) ⇔ R(x) = 0

Vamos ver como funciona a divisão pelo método das chaves

Vamos dividir x⁴ + 2x³ – x + 3 por x² – x

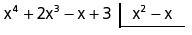
O processo se dá sempre iniciando a divisão do monômio de maior grau do dividendo pelo monômio de maior grau do divisor.

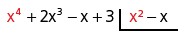
Faremos a divisão de x⁴ por x², ou seja ^x4/_x2 = x²

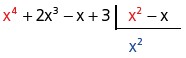
Posteriormente o resultado da divisão será multiplicado por todos os monômios do divisor e será subtraído do dividendo (sinal trocado após o produto)

x²(x² – x) = x⁴ – x³

Ao trocarmos os sinais será –x⁴ + x³

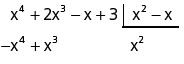
Nessa parte do processo o monômio de maior grau do dividendo, no momento, sempre será anulado.

E dessa forma o processo se repete até que o resultado da subtração tenha grau inferior ao grau do divisor.

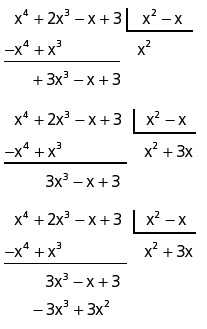
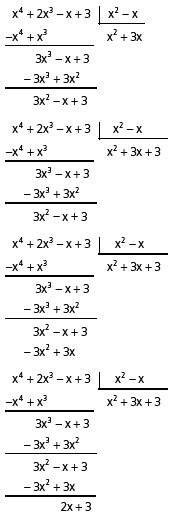
Exemplo:

Determinar o quociente de P(x) = x⁴ + x³ – 7x² + 9x – 1 por D(x) = x² + 3x – 2.

Resolução:

Aplicando o método da chave, temos:

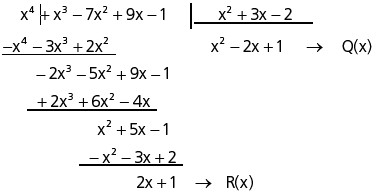
Verificamos que

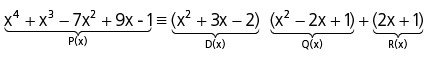
DIVISÃO DE UM POLINÔMIO POR UM BINÔMIO DA FORMA ax + b

Vamos calcular o resto da divisão de P(x) = 4x² – 2x + 3 por D(x) = 2x – 1.

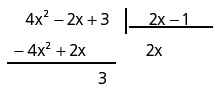
Utilizando o método da chave temos:

Logo: R(x) = 3

A raiz do divisor é 2x – 1 = 0 ⇒ x =¹/₂ .

Agora calculamos P(x) para x =¹/₂ .

P(¹/₂) = 4(¹/₄) – 2(¹/₂) + 3 ⇒ P(¹/₂) = 3

Observe que R(x) = 3 =P (¹/₂)

Portanto, mostramos que o resto da divisão de P(x) por D(x) é igual ao valor numérico de P(x) para x =¹/₂, isto é, a raiz do divisor.