A forma trigonométrica se torna mais usual para operações de produto e divisões e quase que fundamental para potências e radiciações. Vamos supor para todos os casos
Z1 = |Z1| (cis θ1)
Z2 = |Z2| (cis θ2)
I. Produto
Z1 · Z2 = |Z1| |Z2| (cis (θ1 + θ2))
II. Divisão

Tanto o produto quanto a divisão de números complexos na forma trigonométrica resultam em translações no plano de Argand-Gauss.
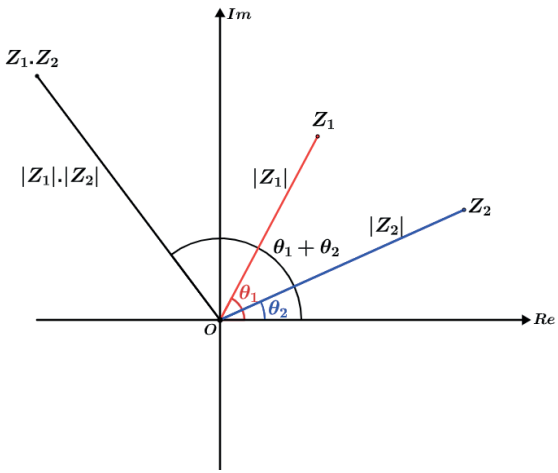
|Z1| >1 e |Z2| >1 → |Z1| · |Z2| > max {|Z1| , |Z2|}
|Z1| >1 e |Z2| <1 ou |Z1|<1 e |Z2| >1 → |Z1| · |Z2| < max {|Z1| , |Z2|}
|Z1| <1 e |Z2| <1 → |Z1| · |Z2| <min {|Z1| , |Z2|}
III. Potenciação (1ª Fórmula de Moovrie)
(Z1)n = (|Z1|)n · cis (n · θ)
Exemplo: sendo Z = -1 + √3i calcular o valor de Z16
Primeiramente iremos colocar Z na forma trigonométrica

Assim:

Utilizando a 1ª fórmula de Moovrie

Se quisermos novamente a forma algébrica

IV. Radiciação (2ª Fórmula de Moovrie)
Para a radiciação será imprescindível a utilização de (θ + 2kπ) e (θ + 360° · k.)
n√Z1 = (Z1)1/n
z1/n é uma potência e daí poderemos fazer como a 1ª fórmula de Moovrie.

Do argumento (θ+2kπ/n) ou (θ+360°·k/n)podemos perceber que (θ+2kπ/n) = (θ/n + 2kπ/n) e (θ+360°·k/n) = (θ/n + 360°·k/n).
Onde para k ∈ {1, 2, 3,…} o argumento de n√Z1 é uma progressão aritmética de 1º termo θ/n e razão 2π/n ou 360°/n.
Para encontrarmos todas as raízes de n√Z1 faremos k variar dentro do conjunto ∈ {1,2,3,…} até que as raízes comecem a se repetir.
Exemplo:
Para z = -1 – √3i encontrar todas as raízes de 4√Z. Primeiramente encontraremos Z na forma trigonométrica.


Quando utilizamos k = 4 percebemos que encontramos novamente Z0.

Neste exemplo ainda podemos encontrar todas as raízes na forma algébrica Z = a + bi, mas isso não é uma regra visto que nem sempre encontraremos ângulos notáveis ou ângulos que são redutíveis a notáveis, mesmo que por transformações trigonométricas.




