A forma trigonométrica dos números complexos é uma parametrização em função de seu módulo e do seno e do cosseno de seu ângulo com o eixo real.
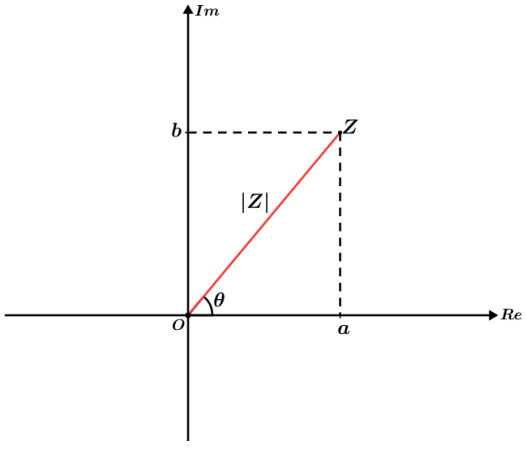
Olhando para o complexo Z = a + bi no plano de Argand-Gauss acima podemos identificar coeficiente da sua parte real a sobre o eixo real e o coeficiente da sua parte imaginária b sobre o eixo imaginário. Dessa forma temos que seu módulo (distância do afixo a origem do plano) é dada por |Z| = √a2+b2.
E dessa forma, quando identificamos o ângulo θ formado entre o módulo de Z e o eixo real, podemos no triângulo retângulo destacado abaixo fazer mais algumas deduções.
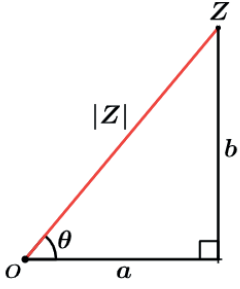
Podemos montar algumas relações trigonométricas
sen θ = b/|Z|
cos θ = a/|Z|
tg θ = b/a
Onde podemos isolar a e b.
b = |Z| sen θ
a = |z| cos θ
Assim, nosso complexo Z, que na forma algébrica é Z=a+bi pode ser escrito como
Z = a + bi = |Z|cosθ + |Z|senθi
Podemos colocar em |Z| evidência
Z =|Z|(cosθ + i · senθ)
Onde acabamos de definir a forma trigonométrica de um número complexo Z.
Para o dia a dia dos cálculos, afim de se não fazer várias vezes a escrita de (cosθ + i· senθ) é aceita a abreviatura de cis θ para (cosθ + i · senθ). Então cisθ = (cosθ + i · senθ).
A forma de escrita mais completa é Z= |Z|(cos(θ + 2kπ) + i · sen (θ+2kπ)) ou Z = |Z|(cos(θ+360°·k) + i · sen (θ+360°·k), porém será mais importante para a operação de radiciação e dessa forma no dia a dia será utilizada majoritariamente a 1ª determinação positiva do ângulo.
A tangente é uma ótima maneira de se descobrir somente o ângulo, ou como definiremos a partir de agora, o argumento de um complexo. Assim utilizando somente tg θ = b/a podemos encontrar o argumento de um complexo, basta somente ter atenção ao quadrante que ele está através dos sinais de a e de b.
a > 0 e b > 0 → 1º quadrante
a < 0 e b > 0 → 2º quadrante
a < 0 e b < 0 → 3º quadrante
a > 0 e b < 0 → 4º quadrante
A base para trabalhar com números complexos na forma trigonométrica é o conhecimento do ciclo trigonométrico, os valores dos ângulos notáveis em todos os quadrantes e suas reduções.
Exemplo:
Passar para a forma trigonométrica o número complexo Z=1-i. Teremos que

Assim teremos que:

Dessa forma, como a > 0 e b < 0 sabemos que o afixo de Z está no 4º quadrante.
Pelos valores de sen θ e cos θ vemos que é o ângulo que quando reduzido do 4º ao 1º quadrante tem seus valores de seno e cosseno iguais ao ângulo de 45°, ou como é mais utilizado, o ângulo em radianos π/4 rad. A relação entre o 4º e o 1º quadrantes é de ângulos replementares, assim θ = 7π/4 rad.

Uma forma mais rápida, que com mais experiência será mais fluída, é colocar |Z| em evidência em relação a Z.

ProBizu
I. Conjugado de Z na forma trigonométrica
Z = | Z | (cisθ) e Z¯= | Z |(cis ( -θ ))
II. Argumentos de reais e imaginários puros