UNIÃO DE CONJUNTOS
Dados dois conjuntos A e B, a união desses dois conjuntos (notase por A∪B) é o conjunto formado por todos os elementos que pertençam a A ou a B.
A∪B={x∣x∈A ou x∈B} ou
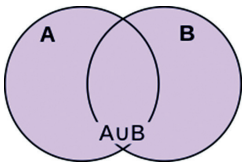
Exemplo: A={1,2,3} e B={3,4}⇒A∪B={1,2,3,4}
Propriedades:
Considere A, B e C conjuntos quaisquer, logo:
- A∪A=A
- A∪B=B∪A
- A∪∅=∅∪A=A
- A∪(B∪C)=(A∪B)∪C
INTERSEÇÃO DE CONJUNTOS
Dados dois conjuntos A e B, a interseção desses dois conjuntos (nota-se por A∩B) é o conjunto formado por todos os elementos que pertençam a A e a B.
A∩B={x∣x∈A e x∈B} ou
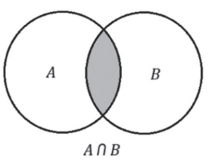
Exemplo:
A={1,2,3} e B={3,4}⇒A∩B={3}
Atenção: dois conjuntos são chamados de disjuntos quando sua interseção é vazia, ou seja, A∩B=∅.
Propriedades:
Considere A, B e C conjuntos quaisquer, logo:
- A-A=∅
- A-∅=A
- ∅-A=∅
- A-B≠B-A
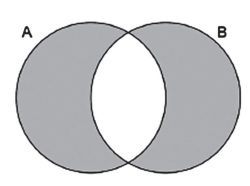
Observação: Se A-B=B-A então A=B, logo A-B=B-A=∅.Diferença Simétrica de dois conjuntos A e B (nota-se por A Δ B) é o conjunto formado pelos elementos que pertencem à união dos dois conjuntos, mas não pertencem à interseção dos dois conjuntos, ou seja,
A Δ B=(A-B)∪(B-A) ou A Δ B=(A∪B)-(A∩B) ou
COMPLEMENTAR DE B EM A
Dados dois conjuntos A e B, tais que B⊂A, o complementar do conjunto B no conjunto A é o próprio conjunto A-B, ou seja, é o conjunto formado todos os elementos de A que não pertençam a B.
CAB=A-B={x∣x∈A e x∉B} ou
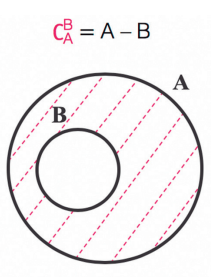
Exemplo:
A={1,2,3,4,5} e B={3,4}⇒CAB=A-B={1,2,5}
Propriedades:
Considere A, B e C conjuntos quaisquer, logo:
- CAA=A-A=∅
- CA∅=A-∅=A
- CAB∩B=(A-B)∩B=∅
- CAB∪B=(A-B)∪B=A
- CACAB=A-(A-B)=B
- CA(B∩C)=A-(B∩C)=(A-B)∪(A-C)=CAB∪CAC
- CA(B∪C)=A-(B∪C)=(A-B)∩(A-C)=CAB∩CAC
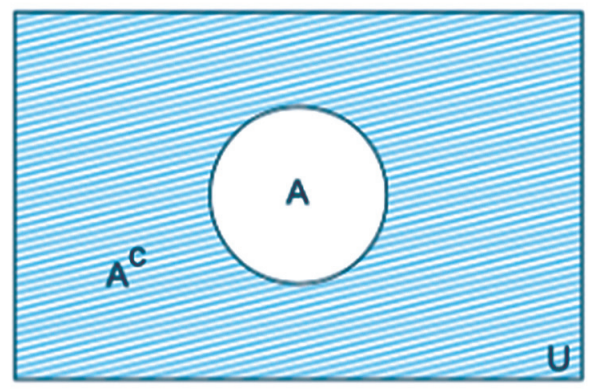
Observação: Negação de um conjunto, ou seja, todos os elementos que estão fora do conjunto A.
A¯=U-A=AC=CA={x∣x∉A} ou
Propriedades finais:
- A∪(B∩C)=(A∪B)∩(A∪C). Propriedade distributiva da união em relação à interseção.
- A∩(B∪C)=(A∩B)∪(A∩C). Propriedade distributiva da interseção em relação à união.
- A∩B¯=A¯∪B¯ ou (A∩B)C=Ac∪Bc. Lei de Morgan.
- A∪B¯=A¯∩B¯ ou (A∪B)C=AC∩BC. Lei de Morgan.
- (A∪B)-C=(A-C)∪(B-C).
- (A∩B)-C=(A-C)∩(B-C).
- (A Δ B)∪C=(A Δ C)∩(B Δ C).
- (A Δ B)∩C=(A Δ C)∪(B Δ C).




