CONJUNTO UNITÁRIO
Chama-se de conjunto unitário todo conjunto que possui um único elemento.
Exemplo:
P= conjunto dos números primos e pares
P={2}
CONJUNTO VAZIO
Chama-se de conjunto vazio todo conjunto que não possui elementos. Representa-se por ou ∅.
O conjunto representado por {∅} é unitário e não vazio.
Exemplo:
P= conjunto dos divisores de 21 e pares
Dℕ(21):1,3,7,21
Logo, P=∅
SUBCONJUNTOS
Um conjunto A é subconjunto de um conjunto B se, e somente se, todo elemento de A é também elemento de B. Denota-se por A⊂B (lê-se A está contido em B) esta relação de inclusão do conjunto A em B ou por B⊃A (lê-se B contém A). Não havendo a inclusão nos conjuntos, usa-se ⊄ (não está contido) e ⊅(não contém).
A ⊂ B⇔(∀x)(x ∈ A ⇒ x ∈ B) ou
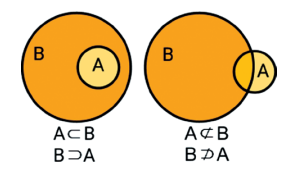
Exemplo:
A={1,2,3} e B={1,2,3,4,5}, logo A⊂B ou B⊃A.
C={a,b} e D={b,c}, logo C⊄D ou D ⊅C.
Propriedades da inclusão:
Considere os conjuntos A, B e C conjuntos quaisquer, logo:
- ∅⊂A. O conjunto vazio é subconjunto de qualquer conjunto.
- A⊂A. O subconjunto mais amplo que um conjunto pode ter é ele próprio.
- A⊂B e B⊂C⇒A⊂C. Propriedade transitiva.
- A⊂B e B⊂A⇒A=B ou A=B⇔(∀x)(x∈A⇔x∈B). Igualdade de conjuntos.
Observação: Subconjunto próprio de um conjunto A é todo subconjunto diferente do próprio conjunto A.




