“Marcos é médico e Maria é estudante”, poderemos representá-la apenas por:
p ꓥ q
onde: p = Marcos é médico e q = Maria é estudante.
O valor lógico de uma proposição conjuntiva é descoberto da seguinte maneira: uma conjunção só será verdadeira, se ambas as proposições componentes forem também verdadeiras. Então, na sentença “Marcos é médico e Maria é estudante”, só podemos concluir que essa proposição composta é verdadeira se for verdade, ao mesmo tempo, que Marcos é médico e que Maria é estudante.
Pensando pelo caminho inverso, temos que basta que uma das proposições componentes seja falsa, e a conjunção será – toda ela – falsa. Certamente o resultado falso também ocorre quando ambas as proposições componentes forem falsas. Essas conclusões podem ser resumidas em uma tabela (tabela-verdade). Sejam as premissas:
p = Marcos é médico e q = Maria é estudante.
Se considerarmos que ambas são verdadeiras, a conjunção formada por elas (Marcos é médico e Maria é estudante) será também verdadeira. Teremos:
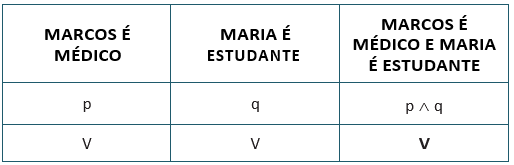
Se for verdade apenas que Marcos é médico, mas falso que Maria é estudante, teremos:
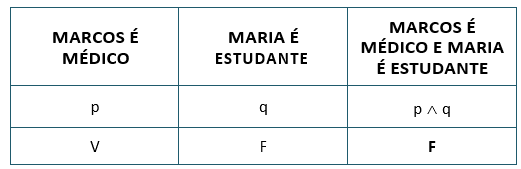
Por outro lado, se for verdadeiro que Maria é estudante, e falso que Marcos é médico, teremos:
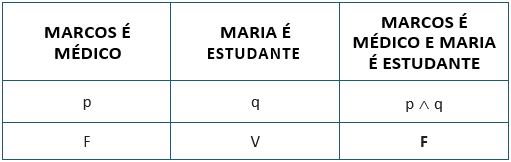
Enfim, se ambas as sentenças simples forem falsas, teremos que:
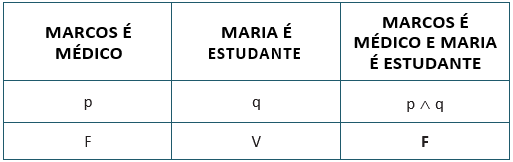
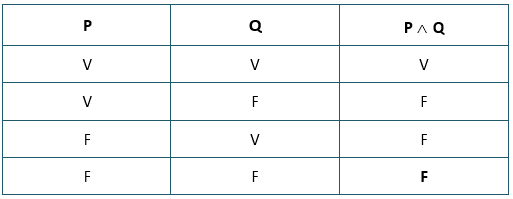
As quatro situações exprimem todas as possibilidades para uma conjunção. Veremos a seguir, a Tabela-verdade que representa uma conjunção, ou seja, a tabela-verdade para uma proposição composta com a presença do conectivo “e”.
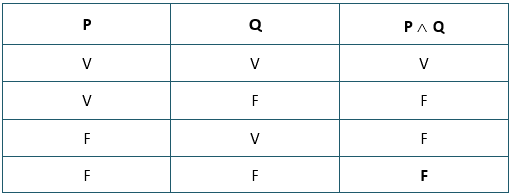
É preciso que a informação da terceira coluna fique em nossa memória: uma conjunção só será verdadeira, quando ambas as partes que a compõem também forem verdadeiras. E falsa nos demais casos.
Uma maneira de assimilar bem essa informação seria pensarmos nas sentenças simples como promessas de um pai a um filho: “eu te darei uma bola e te darei uma bicicleta”. Ora, pergunte a qualquer criança! Ela vai entender que a promessa é para os dois presentes. Caso o pai não dê nenhum presente, ou dê apenas um deles, a promessa não terá sido cumprida. Será, portanto, falsa! Entretanto, a promessa será verdadeira se as duas partes forem também verdadeiras! Na hora de formar uma tabela-verdade para duas proposições componentes (p e q), devemos saber que a tabela terá cinco linhas. Começamos, então, fazendo a seguinte estrutura:
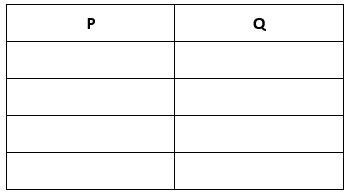
A coluna da primeira proposição terá a seguinte disposição: dois “vês” seguidos de dois “efes”. Assim:
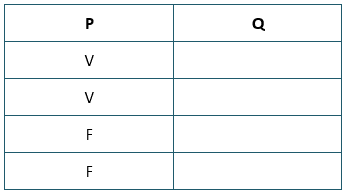
Enquanto a variação das letras (V e F) para a premissa p ocorre de duas em duas linhas, para a premissa q é diferente: “vês” e “efes” se alternando a cada linha, começando com um V. Assim:
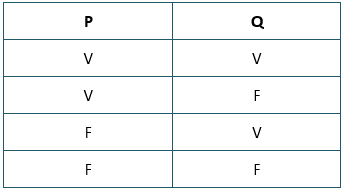
Esta estrutura inicial é sempre assim, para tabelas-verdade de duas proposições p e q. A terceira coluna dependerá do conectivo que as une, e que está sendo analisado. No caso do conectivo “e”, ou seja, no caso da conjunção, já aprendemos a completar a tabela verdade:
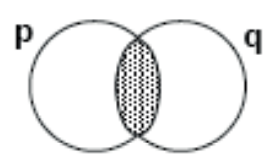
Se as proposições p e q forem representadas como conjuntos, por meio de um diagrama, a conjunção “p e q” corresponde à interseção do conjunto p com o conjunto q. Assim:
p ꓵ q