Se um elemento x pertence a um conjunto P, diz-se que x∈p. Consequentemente, se um elemento x não pertence a P, diz-se que x∉p. Os símbolos ∈ e ∉ são utilizados para a relação de pertinência entre elemento e conjunto.
É coerente adotar letra maiúscula para nomear um conjunto e letras minúsculas para seus elementos. Os conjuntos podem ser representados com os elementos dispostos entre um par de chaves ou com os elementos dispostos no interior de uma linha fechada (diagrama de Venn).
Exemplo
Representação extensa: V={a,e,i,o,u} ou
Representação gráfica (Diagrama de Venn):
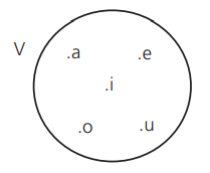
Exemplo:
Descrição do conjunto pela citação dos elementos:
A = conjuntos dos números primos
A = {2,3,5,7,11,13,17,…}
Exemplo:
Descrição do conjunto por uma propriedade:
B = {x|x é divisor de 6}
B = {-6,-3,-2,-1,1,2,3,6}
Como se pode observar nos exemplos, um conjunto pode ser finito, ou seja, com um número limitado de elementos ou infinito, ou seja, com um número ilimitado de elementos.




