Durante a subida o movimento é retardado (o corpo é “freado” pela “aceleração da gravidade”). No topo da trajetória há a inversão do movimento e v = 0. A força gravitacional continuará agindo sobre o corpo com |a| = g até que o corpo retorne ao seu ponto de partida ou ao solo (Não necessariamente um corpo precisa ser arremessado para cima a partir do solo).
Durante a descida, sob a aceleração da gravidade, o corpo cairá em queda livre.
Durante o movimento de subida e de descida temos |a| = g, porém para efeitos de equacionamento, em ambos os movimentos, a = – g.
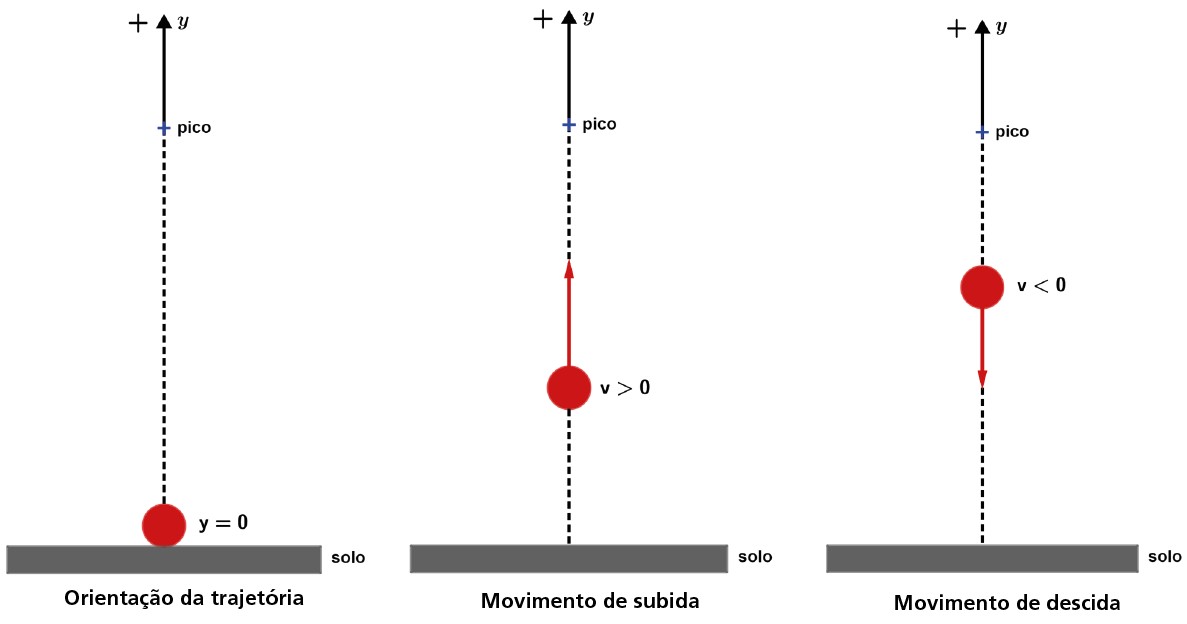
Repare que em ambos os movimentos a aceleração é contrária a orientação que determinamos (do solo para cima). Vamos chamar a altura atingida pelo corpo de H e a altura inicial do lançamento de H0.

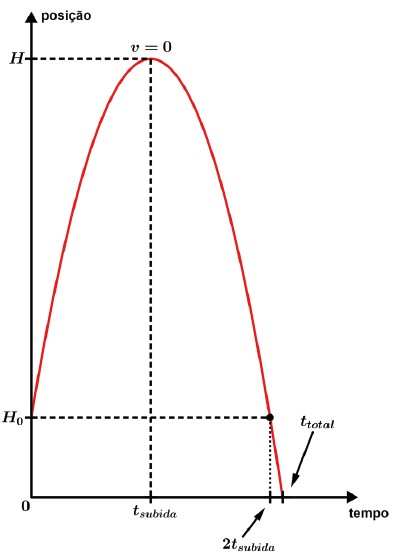
No pico da trajetória temos v = 0 e temos que o tempo de subida é igual ao tempo de descida. Mas tome cuidado com o ponto de início do lançamento, vamos ver pelo diagrama posição x tempo a diferença de um lançamento a partir do solo e um lançamento de uma altura acima do solo, mas que o corpo retorna para o solo.
- Lançamento vertical para cima iniciando no solo e retornando para o solo
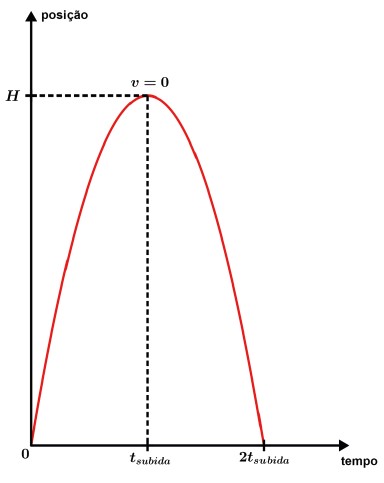
- Lançamento vertical para cima iniciando de uma altura acima do solo e retornando para o solo
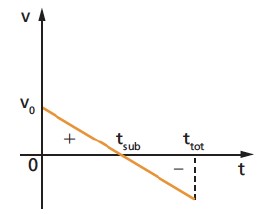
- Diagrama velocidade x tempo
Exercício Resolvido 1: Abandona-se uma bolinha de tênis em queda livre com a intenção de que ela caia exatamente dentro de um pequeno vaso sobre um carrinho. Este se desloca para a direita em MRU, aproximando-se da reta vertical (trajetória da bolinha) com velocidade escalar v = 4 m/s. Admita que a figura nos mostre a posição dos corpos no instante t = 0.
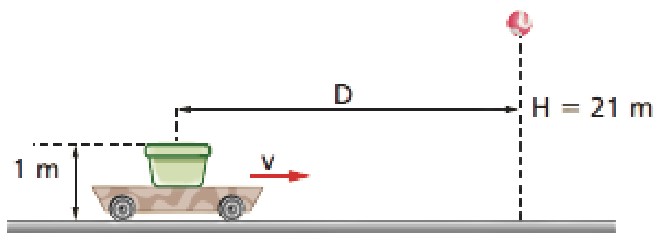
Adotando g = 10 m/s², determine:
a) o instante T em que o vaso deve chegar à reta vertical, que compõe a trajetória da bolinha;
b) a distância D indicada.
Resolução: Orientemos a trajetória da bolinha para baixo.
H = 21 – 1 = 20 m
a) A equação horária das posições da bolinha é dada por:

Temos: v0 = 0

A bolinha deverá percorrer apenas 20 m para que se tenha sucesso total no evento. Portanto, façamos na equação horária y = 20 m e chamaremos o instante final de T: 20 = 5T².

b) O carrinho está em MRU com velocidade escalar v = 4 m/s:
D = V · T ⇒ D = 4 · 2 ⇒ D = 8 m
Exercício Resolvido 2: Uma pequena esfera de aço foi lançada verticalmente para baixo, com velocidade de módulo 4,0 m/s, num local onde se pode desprezar a resistência do ar. Tendo percorrido uma distância h, medida a partir do ponto de lançamento, sua velocidade passou a ter módulo de 8,0 m/s. 0 módulo da aceleração da gravidade é g = 10 m/s². Determine a distância h.
Resolução: Da equação de Torricelli: v2 = v20 + 2aΔS
Sendo a = g, a equação fica:





