MOVIMENTOS SIMULTÂNEOS
Movimentos simultâneos são aqueles que acontecem de maneira independente um do outro mas que os tempos estão atrelados um ao outro.
Exemplo: Uma pessoa está de pé na extremidade esquerda de um ônibus, como na figura, pois este se encontra próximo ao ponto que a pessoa irá descer. O ônibus, que possui 10 m de comprimento e velocidade escalar constante de 72 km/h, ingressa no trajeto AB no mesmo instante em que a pessoa começa a se deslocar, com velocidade escalar constante de 4 m/s, no mesmo sentido de deslocamento do ônibus. No instante em que o ônibus deixa completamente o trecho AB, a pessoa atinge a outra extremidade do ônibus. Diante disso responda as perguntas abaixo.
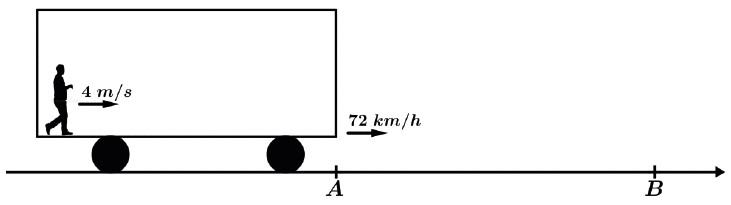
a) Quanto tempo durou a caminhada da pessoa?

b) Determine o comprimento AB.

O tempo de deslocamento da pessoa será o mesmo tempo necessário para o ônibus percorrer o trajeto AB.

c) Determine a distância total percorrida pela pessoa, medida em relação ao solo, enquanto o ônibus atravessava completamente o trecho AB.
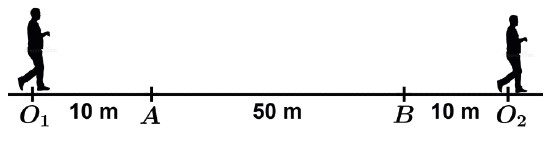
70 m
VELOCIDADE RELATIVA
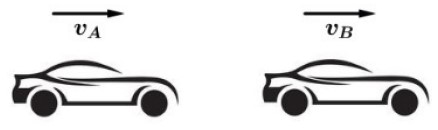
Dois móveis A e B estando em uma mesma trajetória retilínea, com velocidades escalares constantes e respectivamente iguais a VA e VB teremos.
A E B NO MESMO SENTIDO
|VR| = |VA – VB|
A E B EM SENTIDOS CONTRÁRIOS
|VR| = |VA + VB|
No caso de A e B estarem em sentidos contrários a velocidade relativa se dá tanto no caso dos móveis estarem se aproximando como se afastando.


Exemplo: encontre a velocidade relativa em cada situação abaixo.
a)
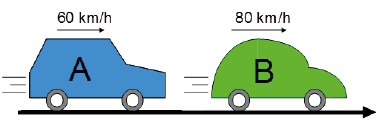
|VR| = |VA – VB| = |60 – 80| = |-20| = 20 km /h
b)

|VR| = |35 + 15| = |50| = 50 m / s
c)

|VR| = |108 + 72| = |180| = 180 km /h
Vamos ver um exemplo utilizando o conceito de velocidade relativa.
Imagine que numa corrida um casco é atirado em direção ao carro do Mário. No instante t = 0 o caso e o carro do Mário estão a 200 m de distância um do outro e com velocidades escalares constantes iguais a 50 m/s e a 40 m/s respectivamente.
a) Quanto tempo levará até o casco acertar o carro do Mário?
b) Quantos metros Mário ainda percorreu até ser atingido?

Resolução:
a) Se utilizarmos o conceito de velocidade relativa, pelo fato de as partículas estarem no mesmo sentido do movimento teremos
vR = vC – vM = |50 – 40| = 10 m/s
Podemos considerar Mário parado e somente o casco indo em direção a Mário com velocidade escalar constante de 10 m/s.
Assim o casco deve percorrer 200 m até a colisão e assim

b) Mário estava se movimentando com velocidade escalar constante de 40 m/s e permaneceu dessa forma durante 20 s e assim
ΔS = vM · t = 40 · 20 = 800 m
Se Mário ainda percorreu 800 m o casco, que se encontra a 200 m de distância, percorreu 1000 m até a colisão. Vamos confirmar?
ΔS = vc · t = 50 · 20 = 1000 m
Observação: No diagrama de velocidade × tempo podemos encontrar o deslocamento de um móvel através da área abaixo da reta.
ΔS = v . Δt = v(t2 – t1)
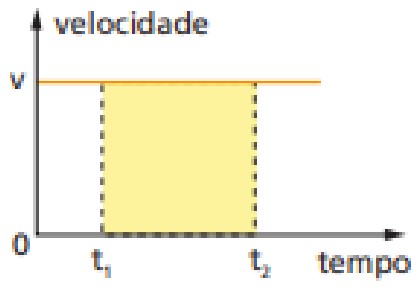
Da geometria temos, destacado em amarelo, um retângulo de base e altura v. Podemos calcular a área do retângulo por
Á Área = (t2 – t1) · v
Sendo assim podemos afirmar que a área do retângulo formado no diagrama de velocidade x tempo do movimento uniforme é numericamente igual ao deslocamento de um móvel.
ΔS ≡ Área
Exercício Resolvido 1: Dois trens, A e B, de 200 m de comprimento cada um, correm em linhas paralelas com velocidades escalares de valores absolutos 50 km/h e 30 km/h, no mesmo sentido. A figura mostra o instante em que o trem A começa a ultrapassar o trem B. Depois de quanto tempo terminará a ultrapassagem?
Resolução: Vamos resolver este exercício pela velocidade relativa. A velocidade escalar de A em relação a B tem valor absoluto:
Vrel = 50 km/h – 30 km /h
Vrel = 20km /h
Assim, cada ponto do trem A percorre: 200 m + 200 m = 400 m = 0,400 km com velocidade relativa 20 km/h.

Exercício Resolvido 2: A figura representa as posições de dois móveis, A e B, no instante t = 0. Os móveis A e B possuem movimentos uniformes cujas velocidades escalares têm valores absolutos 15 m/s e 10 m/s, respectivamente. Depois de quanto tempo A e B vão se encontrar?
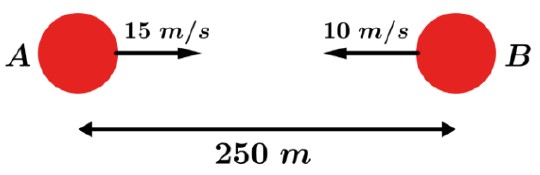
Resolução: Vamos adotar como origem das abscissas a posição inicial de A e orientar a trajetória de A para B. Desse modo: SOA = 0 e SOB = 250 m.
A velocidade escalar de A é positiva, mas a de B é negativa, pois seu movimento é retrógrado: VA = 15 m/s e VB = -10 m/s
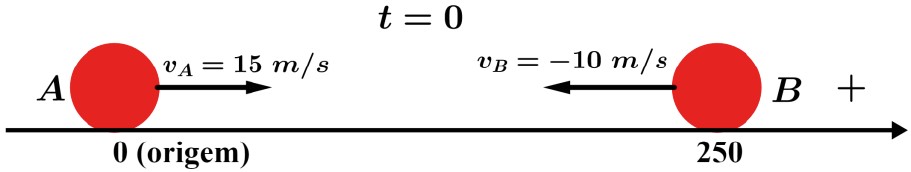

No encontro, temos:
SA = SB ⇒ 15t = 250 – 10t ⇒ 15t + 10t = 250 ⇒ 25t = 250 ⇒ t = 10 s
Exercício Resolvido 3: Dois automóveis percorrem uma mesma estrada retilínea em sentidos opostos. Num dado instante suas abscissas são -12 m e +18 m, como indica a figura. Os módulos de suas velocidades permanecem constantes, sendo: |v1| = 10 m/s e |v2| = 5,0 m/s.
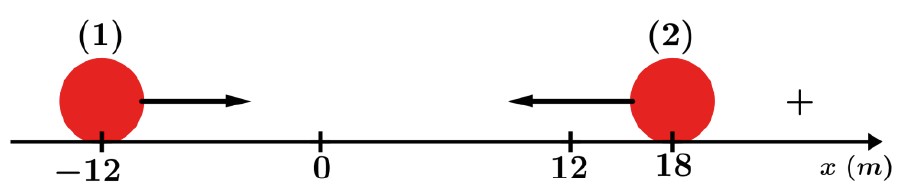
a) Escreva as respectivas equações horárias de seus movimentos.
b) Determine o instante e a posição do encontro.
c) Em que instante eles estarão a 60 m um do outro?
Resolução:
a) S1 = S01 + v01 · t = -12 + 1t e S2 = S02 + v2 · t = 18 – 5t
b) S1 = S2 ⇒ -12 +1 t = 18 – 5 t ⇒ 6 t= 30 ⇒ t = 5 sS1 = -12 + t = -12 + 5 = -7
c) |S2 – S1| = 60 ⇒ 18 – 5t – (-12 + t) |= 60 ⇒| 18+ 12 – 5t – t| = 60 ⇒ | 30 – 6 t| = 60 ⇒30 – 6 t = 60 ou 30 – 6 t = -6030 – 6 t = 60 ⇒ – 6 t = 30 ⇒ t = -5 s (impossível) 30 – 6 t = -60 ⇒ – 6t = – 90 ⇒ t = 15s




