DESLOCAMENTO ANGULAR
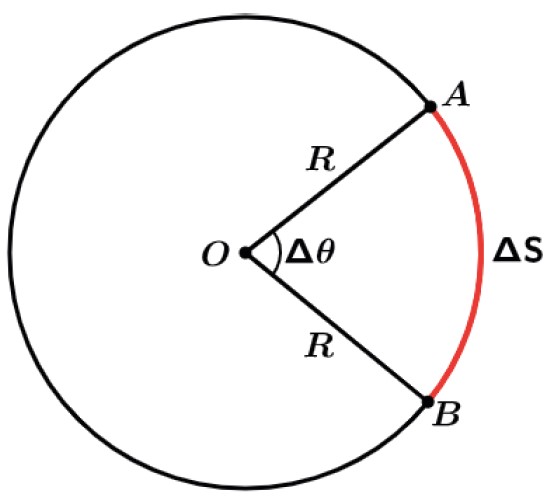
Na figura abaixo temos uma partícula que se deslocou do ponto A para o ponto B sobre uma circunferência de centro O e raio R. O comprimento ΔS do arco AB^ é o espaço percorrido pela partícula, e o ângulo central Δθ oposto ao arco AB é o deslocamento angular
Em alguns casos vamos utilizar o sentindo anti-horário como positivo e o sentido horário como negativo, como na trigonometria.
VELOCIDADE ANGULAR
Se uma partícula, em movimento circular, executa um deslocamento angular Δθ em um intervalo Δt possui velocidade angular média (ωm).

Observação: Se tivermos um corpo rígido em rotação, a velocidade angular média do corpo, isto é, todos os pontos do corpo terão a mesma velocidade angular.
VELOCIDADE ANGULAR E ESCALAR
A velocidade escalar média é dada por vm = ΔS/Δt e vimos também que o comprimento de um arco de circunferência pode ser calculado como

Sendo assim

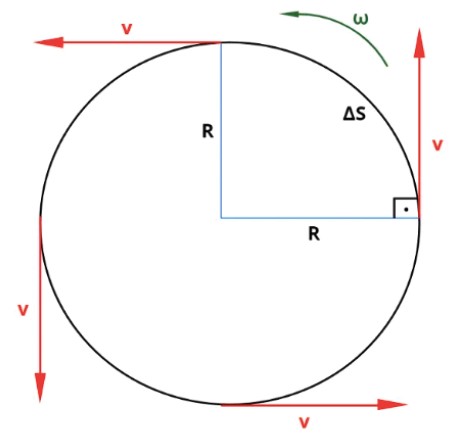
A velocidade é perpendicular a trajetória.
EQUAÇÃO HORÁRIA DA POSIÇÃO ANGULAR NO MCU
Tomando OO’ como referência para o movimento de uma partícula sobre uma circunferência.
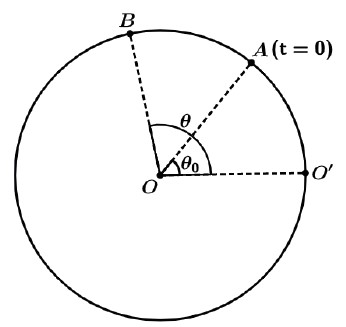
Seja o ponto A a posição de início (t = 0) de movimento de uma partícula e o ponto B a posição final do movimento.
Assim como no movimento retilíneo temos S = S0 + v⋅t teremos

Exemplo: Uma partícula move-se sobre uma circunferência descrevendo um arco PQ¯, que corresponde a um ângulo central ∆θ = 120º, em um intervalo de tempo ∆t = 2 segundos. Calcule a velocidade angular média da partícula nesse intervalo de tempo, em rad/s.
Resolução:

Exemplo: Uma partícula move-se sobre uma circunferência de centro O, com velocidade angular constante w = 5,0 rad/s, como ilustra a figura.
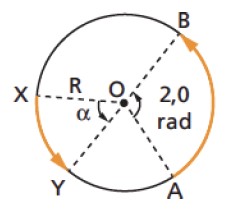
Calcule:
a) o intervalo de tempo gasto pela partícula no percurso AB;
b) a medida do ângulo a, sabendo que o trecho XY é percorrido em 0,30 s.
Resolução:
Resolução:
a) No percurso AB temos ∆θAB = 2,0 rad e a velocidade angular da partícula ω = 5,0 rad/s.

PERÍODO E FREQUÊNCIA
Considere um corpo girando com velocidade angular constante ou uma partícula em movimento circular uniforme. Nesses casos, o intervalo de tempo correspondente a uma volta é sempre o mesmo e é chamado de período do movimento, sendo usualmente representado por T. A frequência (f) desse movimento é o número de voltas por unidade de tempo:

A frequência é dada em voltas ou revoluções por unidade de tempo. Por exemplo revoluções por hora, revoluções por minuto, revoluções por segundo, etc. No SI a unidade da frequência é o hertz (Hz) que é igual a uma revolução por segundo.
Se considerarmos T o intervalo de tempo necessário para que a partícula execute uma revolução completa teremos f = 1/T

Podemos relacionar a velocidade escalar e a velocidade angular com o período e a frequência de um movimento circular uniforme.
No movimento circular temos que uma revolução completa equivale a 2π rad e dessa forma o intervalo de tempo ∆θ será o período T.

Exemplo: Uma pequena pedra amarrada a uma das extremidades de um fio inextensível de 1m de comprimento, preso a um galho de árvore pela outra extremidade, oscila sob ação do vento entre dois pontos equidistantes e próximos a vertical. Durante 10 s, observou-se que a pedra foi de um extremo ao outro, retornando ao ponto de partida, 20 vezes. Calcule a frequência de oscilação desse pêndulo.
Resolução:

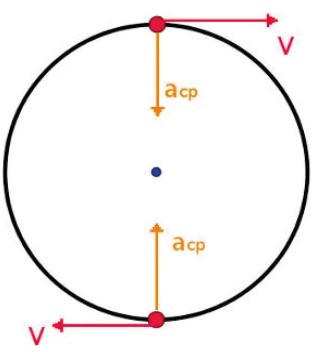
ACELERAÇÃO NO MOVIMENTO CIRCULAR UNIFORME
Uma partícula está em movimento circular quando está sob uma força de módulo constante e de direção perpendicular à velocidade, de forma que o módulo dessa velocidade se mantenha constante, alterando somente sua direção e seu sentido. A força aplicada nesse caso é denominada força centrípeta.
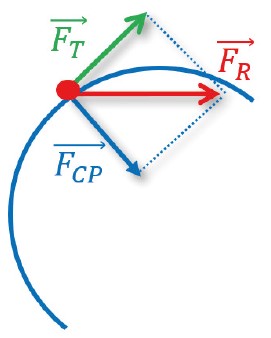

Quando a partícula está em movimento circular uniforme (MCU) seu movimento será acelerado. Nesse caso, a aceleração que o corpo sofre é centrípeta e aponta sempre para o centro de sua trajetória, na direção de seu raio.