TRANSMISSÃO DE VELOCIDADE LINEAR
De modo geral, os vários dispositivos de transmissão de movimento circular encaixam-se em um dos dois casos esquematizados abaixo.
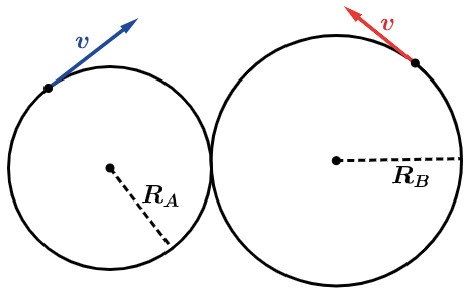
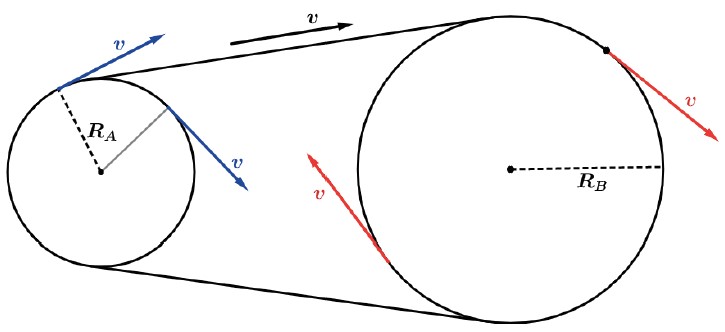
Nos dois casos, para que não haja escorregamento, os pontos das periferias das duas rodas devem ter a mesma velocidade linear v.
ωA · RA = ωB · RBfA · RA = fB · RB
A velocidade linear de A é igual à de B:
VA = VB
A polia com maior raio terá menor frequência e maior período. Podemos encontrar uma relação através da equação:

TRANSMISSÃO DE FREQUÊNCIA
Esse acoplamento é feito através de um eixo que liga as polias pelos seus centros, como a figura abaixo. Quando o eixo gira, ambas as polias giram com a mesma frequência, assim:
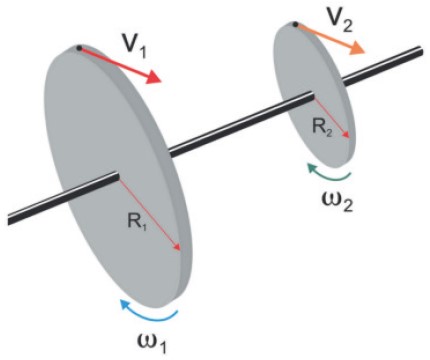
As velocidades angulares, frequências e períodos serão os mesmos
ω1 = ω2, f1 = f2 e T1 = T2
No entanto, a polia maior terá maior velocidade linear, pois v = ωR. Podemos relacionar as velocidades das duas polias através da equação:

Exemplo: A figura ilustra duas polias acopladas por uma correia. A polia A, de raio 12 cm, gira no sentido horário com velocidade angular 50 rad/s. A polia B tem raio 30 cm.

a) Em que sentido gira a polia B?
b) Qual é a velocidade angular da polia B?
Resolução:
a) Horário
b) ωA · RA = ωB · RB ⇒ 50 · 15 = ωB · 30 ⇒ ωB = 25 rad/s
Exemplo: As rodas dentadas têm raios RA = 15 cm e RB = 20 cm. Sabe-se que a roda A gira no sentido horário com frequência 40 Hz.

a) Em que sentido gira a roda B?
b) Qual é a frequência do movimento de B?
Resolução:
a) Anti-horário





