Movimento Harmônico Simples (MHS)

Quando a força resultante que atua em uma partícula apresentar a forma abaixo

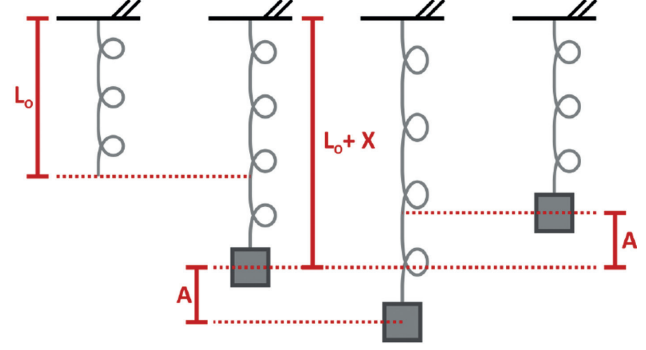
Podemos dizer que a partícula realiza um M.H.S. Vamos imaginar a seguinte situação: uma mola pendurada no teto com a sua outra ponta presa a um bloco de massa m. O sistema está inicialmente em repouso. Ou seja, a mola está esticada e essa elongação x é medida com a equação abaixo:

O que fizemos foi igualar o módulo da força peso ao da força elástica. Vamos lembrar que a força elástica é definida como

O sinal de menos deve-se ao fato de que o sentido da força é oposto ao sentido da deformação da mola. 

Bom, vamos continuar com a nossa situação. Suponha que alguém, após a situação acima, tenha aplicado uma força no bloco de modo que a mola esticasse ainda mais (x+d). Nesse caso a força elástica supera, em módulo, a força peso. Logo após a mola alcançar essa nova posição (L+x+d), onde L é o seu comprimento natural, essa pessoa que aplicou uma força extra no bloco o solta. Como será o movimento da mola?

Sim, será oscilatório. A mola ficará oscilando em torno da posição inicial de equilíbrio (x). Vamos considerar que não há atuação de forças dissipativas. A amplitude do movimento (A) será justamente o quanto a pessoa esticou a mola (d). Sendo assim, o bloco oscilará da posição inicial A, subindo, passando pela posição de equilíbrio e alcançando a posição –A, onde começará a descer, passando novamente pela posição de equilíbrio e voltando para o ponto A. O tempo necessário para uma oscilação completa é chamado de período (T), que é o inverso da frequência (f) de oscilação do movimento, como já sabemos

Um M.H.S. pode ser transformado em um círculo. A analogia ajuda bastante no entendimento do movimento. Observe o círculo a seguir:

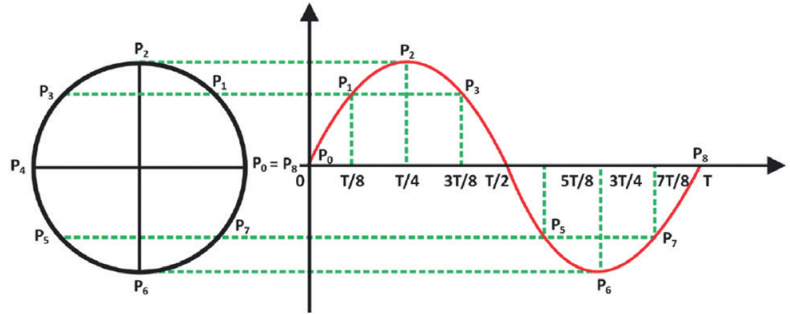
Podemos ver que a movimentação vertical do objeto ao longo de sua trajetória circular é um M.H.S. cujo período é o mesmo do objeto (tempo para dar a volta no círculo) e a amplitude do seu movimento coincide com o raio da trajetória. Sendo assim podemos calcular a velocidade angular (ω) do objeto, afim de descobrirmos o período de oscilação do M.H.S. A partir da figura acima podemos retratar o movimento do bloco na mola, por exemplo. Note que, inicialmente o nosso bloco está na posição x = A. Pelo gráfico podemos tirar a equação da posição de um corpo realizando um M.H.S. em função do tempo:

Perceba que, no caso da figura, a posição inicial é x = 0. No nosso exemplo da mola, o bloco começa na posição x = A, então, de modo mais geral (é mais conveniente), temos que:

Onde θ₀ é a fase inicial do sistema.

Note que, como a posição inicial do bloco é x = A, no nosso exemplo, então: 

Lembrando que ω = 2πf = ^2π/_T. Sabendo a frequência ou o período do movimento, conseguimos determinar a posição do objeto submetido a um M.H.S. em função do tempo. A fase inicial conseguimos descobrir sabendo a posição inicial do corpo e/ou a sua velocidade inicial. Porém, podemos descobrir a velocidade angular de outra maneira. Para isso vamos, a partir da equação da posição, as equações da velocidade e da aceleração em função do tempo:

Observação: a velocidade será nula quando o objeto estiver nos extremos (x = – A e x = + A) e máxima quando estiver na posição de equilíbrio, já que, nesse ponto, a aceleração será nula, ou seja, cos (ωt + θ₀) = 0, portanto, sen (ωt + θ₀) = 1 ou -1. A tabela abaixo apresenta todas essas informações:

A partir da tabela anterior podemos entender como se comportam as energia no movimento e gerar o gráfico abaixo:

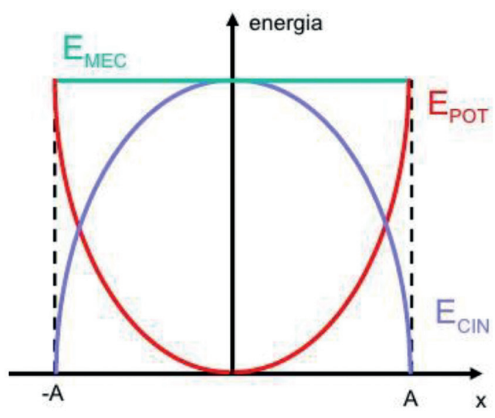
A energia mecânica constante durante o movimento e, conforme a energia potencial cai, a cinética aumenta e vice-versa.

Note também, a partir da tabela, que a aceleração é diretamente proporcional ao deslocamento do objeto: 

Podemos definir a velocidade angular, também chamada de pulsação, do movimento de um bloco de massa m preso a uma mola de constante elástica k sob M.H.S. como:

Outro exemplo muito comum de M.H.S. é o movimento de uma bolinha de massa m presa por um fio cuja outra extremidade está presa no teto. Movimento de um pêndulo simples.

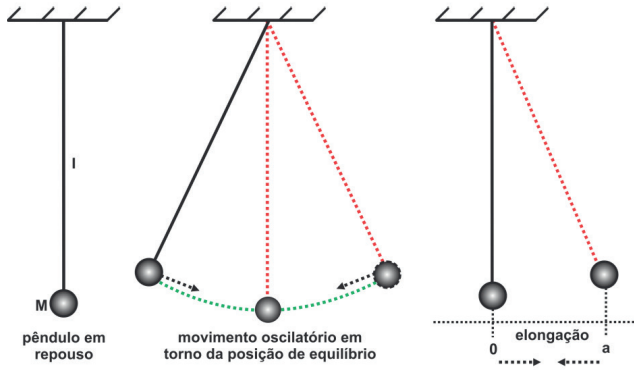
As equações de movimento continuam sendo as definidas anteriormente, já que se trata de um M.H.S. bem como todas as informações da tabela. O que será diferente é a velocidade angular do movimento. Pela figura acima podemos dizer que: 

Exercício Resolvido 1: Um pêndulo cujo comprimento de fio vale 1,0 m foi abandonada a uma distância de 20 cm da posição de equilíbrio. Qual é o período do movimento? E se o pêndulo fosse afastado a uma distância de 10 cm, qual seria o período?

Resolução:

Apesar de ser contra a nossa intuição, o período não depende da amplitude de oscilação. Sendo assim, tanto a 20 cm quanto a 10 cm, o período será:

Observação: Essa fórmula só vale para pequenas oscilações. Mas, para um afastamento de 45°, por exemplo, o erro é menor que 10%. Então, podemos usar essa fórmula sem muitos problemas.