Mistura (ou solução ideal) de líquidos

ENTALPIA DE DISSOLUÇÃO

O processo de dissolução de um soluto num solvente implica da quebra e formação de ligações entre átomos ou íons, no caso das soluções iônicas, entre moléculas, no caso das soluções intermoleculares, e na formação de ligações do tipo, íon dipolo, para solvatar solutos iônicos e intermoleculares, para as soluções moleculares. Esse fato, nos deixa claro que seria, à princípio, um processo que ocorre com absorção ou liberação de calor, gerando um entalpia de dissolução

Exemplo: dissolução do sulfato de lítio, Li₂SO₄:

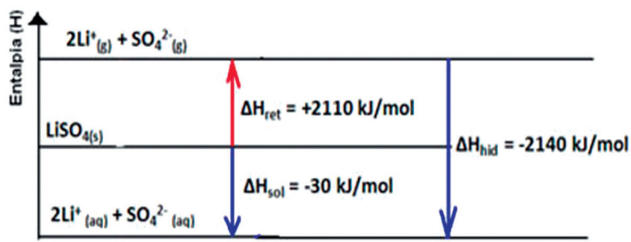
Li₂SO_4 (s) + H₂O_(aq) → Li₂SO_4 (aq) ΔH = -30 kJ × mol^-1

TIPOS DE DISSOLUÇÕES

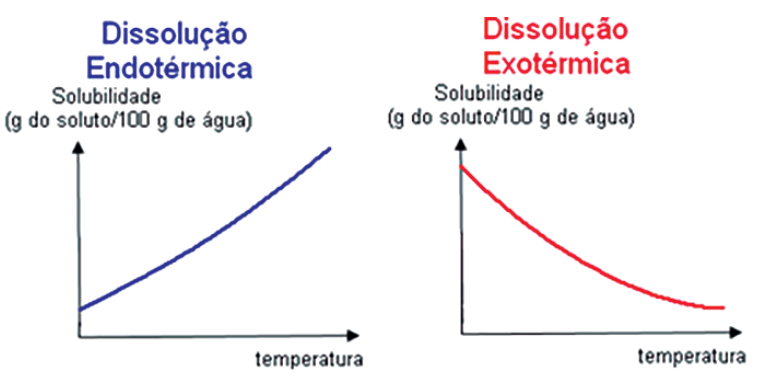
SOLUÇÃO IDEAL

É aquela na qual a entalpia de solução é zero. Todas as forças intermoleculares são iguais, sejam as moléculas semelhantes ou não, onde a variação do volume da mistura também será zero. Quanto mais próxima de zero for o valor da entalpia de solução, mais “ideal” é a solução.

LEI DE RAOULT

“Quando um líquido é acrescentado a uma mistura homogênea e de comportamento ideal, numa dada temperatura, ocorre uma diminuição de sua pressão de vapor proporcional à sua fração molar na mistura na mesma temperatura:

P = x (P°), onde:

P→pressão de vapor do líquido na mistura.
Po→pressão de vapor do líquido puro.
x→fração molar do líquido na mistura.

Como o somatório das frações molares é sempre igual a 1, podemos então concluir que pressão de vapor da mistura é o somatório das novas pressões de vapor obtida por cada líquido misturado.

P(mistura) = P_i + P_j= x_i(P^o)_i + x_j(P^o)_j

A composição de cada substância da mistura na fase vapor pode ser obtida aplicando a Lei de Dalton para os Gases:

y_ie y_j → frações molares das substâncias i e j na fase vapor:

SOLUÇÕES NÃO IDEAIS

Quando na fase líquida, pode originar as misturas azeotrópicas ou azeótropos e quando na fase sólida pode originar as misturas eutéticas ou eutético.

SOLUÇÃO IDEAL E MISTURAS AZEOTRÓPICAS

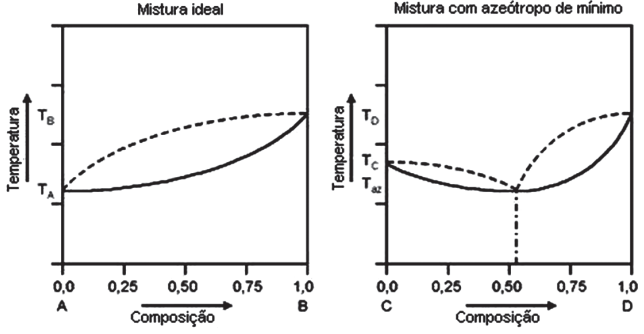
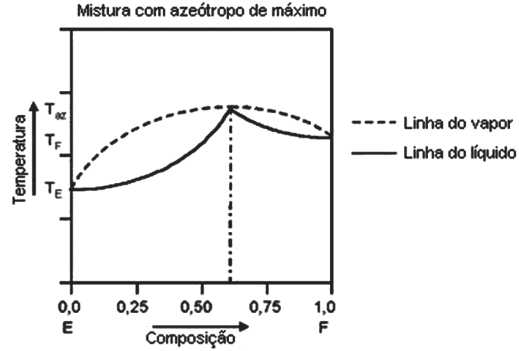
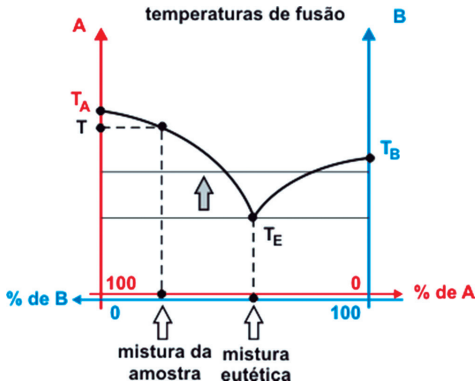
MISTURA EUTÉTICA

As ligas metálicas, onde muitas apresentam comportamento eutético, são misturas de metais que foram misturados na fase líquida e que depois se solidificou por resfriamento, por esse motivo, são também tratadas como soluções, mas tendo a temperatura de fusão como referência de análise.

DESTILAÇÃO FRACIONADA

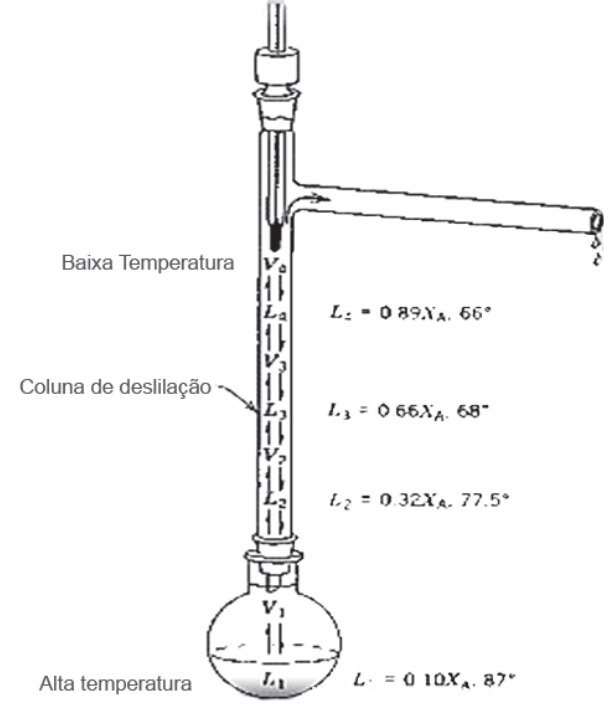
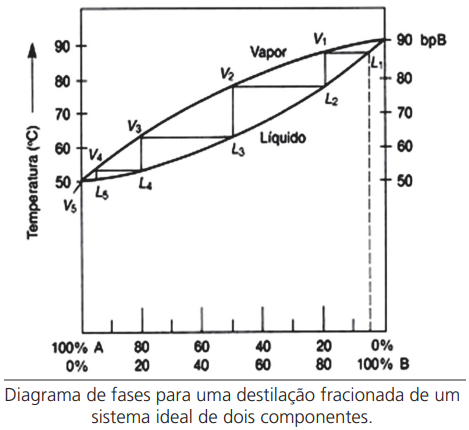
Exemplo: uma mistura líquida homogênea contendo Benzeno e Octano se encontram num laboratório na temperatura de 20º e pressão de 1 atm. A mistura apresenta 20% em massa de benzeno. Considerando as informações contidas na tabela 1 e os dados abaixo, Responda:

a) Qual das misturas poderia apresentar uma maior proximidade de comportamento de solução ideal.

b) Considerando que o calor de vaporização do benzeno é igual a 30,8 KJ ⋅ mol^-1 e que a sua temperatura de ebulição tabelada é de 80,1º C, qual seria a margem de erro para o calcula da sua temperatura de ebulição usando a equação de Clausius-Clapeyron? Dados: Massas molares: Benzeno = 78 g ⋅ mol^-1; Octano = 114 g ⋅ mol^-1.

Resolução:

a) Dados: T = 20ºC ou 293 K; (P^o)benzeno = 76,7 mmHg ou 0,100 atm; (P^o)octano = 10,04 mmHg ou 0,013 atm.

Calculando o número de mols dos componentes para 100g de mistura:

(n)benzeno = 20/78 =0,256 mol; (n) octano = 80/114 = 0,702 mol

Calculando as frações molares dos componentes:

(x) benzeno =[0,256/(0,256+0,702)] = 0,27; (x) octano = 1 – 0,27 = 0,73

Calculando a pressão de vapor da mistura:

(P)mistura = [(x) benzeno · (P°) benzeno] + [(x) octano · (P°) octano] =

=(0,27)(0,100) + (0,73)(0,013) = 0,036 atm

Calculando as frações molares dos componentes na fase gasosa:

[(P) mistura · (y)benzeno] = [(x) benzeno · (P^o) benzeno] →

(y)benzeno=[^{(0,27)(0,100)}/_0,036] = 0,75